해시 테이블
들어가기 전에
- 해시: 해시 테이블에서 입력값을 고정 크기 값으로 매핑하는 과정을 해싱이라고 한다.
- 해시 함수: 해시를 하는데 사용되는 함수. 성능이 좋은 해시 함수들의 특징은 다음과 같다.
- 해시 함수 값 충돌의 최소화
- 쉽고 빠른 연산
- 해시 테이블 전체에 해시 값이 균일하게 분포
- 사용할 키의 모든 정보를 이용하여 해싱
- 해시 테이블 사용 효율이 높을 것
- 로드 팩터: 해시 테이블에 저장된 데이터 개수 n을 버킷의 개수 k로 나눈 것이다.
- 충돌: 해시 값이 같아져 동일한 공간에 같은 값이 선언되는 것이다. 충돌을 해결하기 위한 방법으로 두가지가 있다.
- 개별 체이닝: 키의 해시 값을 계산해 배열의 인덱스를 구한다. 만약 인덱스가 같다면 연결 리스트로 연결한다.
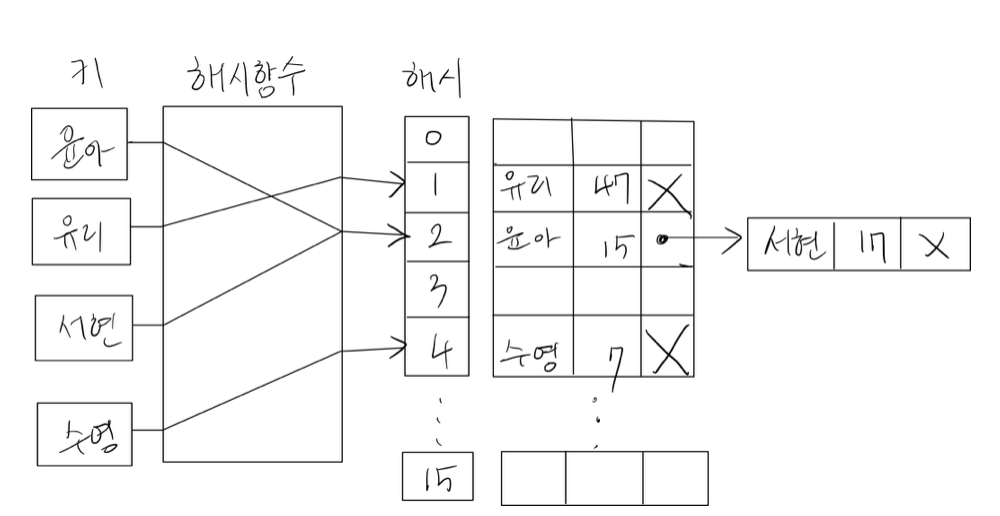
- 개별 체이닝: 키의 해시 값을 계산해 배열의 인덱스를 구한다. 만약 인덱스가 같다면 연결 리스트로 연결한다.
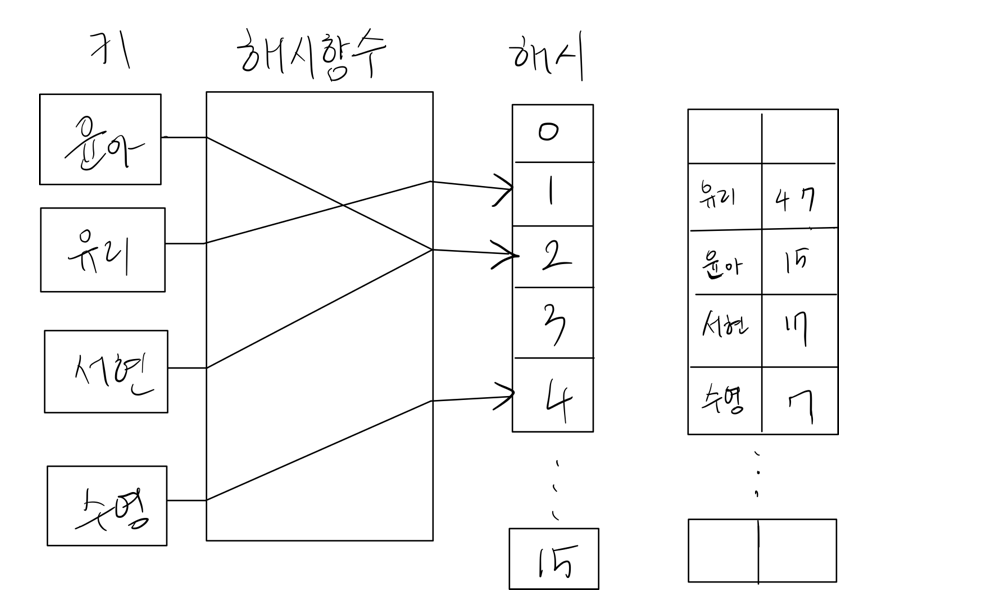
- 오픈 어드레싱: 충돌 발생시 탐사를 위해 빈 공간을 찾아나서는 방식이다. 개별 체이닝과는 다르게 모든 원소를 무한정 저장할 수 없으므로 모든 원소가 반드시 자신의 해시값과 일치하는 주소에 저장된다는 보장은 없다.
Question 28: 해시맵 디자인
put, get, remove 기능을 제공하는 해시맵을 디자인 하라
입력:
[“MyHashMap”, “put”, “put”, “get”, “get”, “put”, “get”, “remove”, “get”]
[[], [1, 1], [2, 2], [1], [3], [2, 1], [2], [2], [2]]
출력:
[null, null, null, 1, -1, null, 1, null, -1]
내 풀이
해시맵에 대한 걔념이 확실하게 잡혀있지 않은 상태에서 일단 풀이를 보류하였다.
풀이 1: 개별 체이닝 방식을 이용한 해시 테이블 구현
class ListNode:
def __init__(self, key=None, value=None):
self.key = key
self.value = value
self.next = None
class MyHashMap:
# 초기화
def __init__(self):
self.size = 1000
self.table = collections.defaultdict(ListNode)
# 삽입
def put(self, key: int, value: int) -> None:
index = key % self.size
# 인덱스에 노드가 없다면 삽입 후 종료
if self.table[index].value is None:
self.table[index] = ListNode(key, value)
return
# 인덱스에 노드가 존재하는 경우 연결 리스트 처리
p = self.table[index]
while p:
if p.key == key:
p.value = value
return
if p.next is None:
break
p = p.next
p.next = ListNode(key, value)
# 조회
def get(self, key: int) -> int:
index = key % self.size
if self.table[index].value is None:
return -1
# 노드가 존재할때 일치하는 키 탐색
p = self.table[index]
while p:
if p.key == key:
return p.value
p = p.next
return -1
# 삭제
def remove(self, key: int) -> None:
index = key % self.size
if self.table[index].value is None:
return
# 인덱스의 첫 번째 노드일때 삭제 처리
p = self.table[index]
if p.key == key:
self.table[index] = ListNode() if p.next is None else p.next
return
# 연결 리스트 노드 삭제
prev = p
while p:
if p.key == key:
prev.next = p.next
return
prev, p = p, p.next
기억해야 할 함수
- collections.defaultdict(): 존재하지 않는 키를 조회할 경우 자동으로 디폴트를 생성해주는 함수이다.
중요 내용
- 파이썬은 오픈 어드레싱 방법을 사용하나 이 풀이 방법은 개별 체이닝 방법으로 풀었다.
- 처음에 해시맵을 만들때 선언하는 해시맵의 크기(버켓의 크기)는 중요하지 않다. 만약 데이터를 넣을 공간이 부족하더라도 같은 인덱스 자리에 연결 리스트로 연결하여 무제한으로 넣을 수 있기 때문이다.
- 만약 연결 리스트를 사용하지 않는다면 넣을 수 있는 데이터의 갯수가 한정되기 때문에 처음에 사이즈 선언을 충분하게 하는 것이 중요하다.
Question 29: 보석과 돌
J는 보석이며, S는 갖고 있는 돌이다. S에 보석이 몇 개가 들어있을까?
입력: jewels = “aA”, stones = “aAAbbbb”
출력: 3
내 풀이
class Solution:
def numJewelsInStones(self, jewels: str, stones: str) -> int:
jewel_list = [jewel for jewel in jewels]
stones_list: Deque = collections.deque([stone for stone in stones])
jewels_count = 0
while len(stones_list) != 0:
if stones_list.popleft() in jewel_list:
jewels_count += 1
return jewels_count
- 보석과 돌을 리스트로 변환한 뒤 큐 방법을 이용해서 풀었다.
- 돌 리스트는 데크를 선언하여 큐 방법을 이용하여 풀 수 있도록 하였다.
- 해시 테이블 방법은 사용하지 않았다.
결과
Runtime: 58 ms, faster than 14.29% of Python3 online submissions for Jewels and Stones. Memory Usage: 13.9 MB, less than 80.19% of Python3 online submissions for Jewels and Stones.
풀이 1: 해시 테이블을 이용한 풀이
class Solution:
def numJewelsInStones(self, J: str, S: str) -> int:
freqs = {}
count = 0
# 돌(S)의 빈도 수 계산
for char in S:
if char not in freqs:
freqs[char] = 1
else:
freqs[char] += 1
# 보석(J)의 빈도 수 합산
for char in J:
if char in freqs:
count += freqs[char]
return count
중요 내용
- 돌 문자열에 들어있는 문자의 횟수를 나타낸 딕셔너리에서 보석 문자열에 나타나는 문자가 몇번 나타나는지 카운팅 하는 방법으로 풀었다.
- 딕셔너리 또한 가장 기본적인 해시 테이블의 형태라고 할 수 있다.
풀이 2: defaultdict를 이용한 비교 생략
class Solution:
def numJewelsInStones(self, J: str, S: str) -> int:
freqs = collections.defaultdict(int)
count = 0
# 비교 없이 돌(S) 빈도 수 계산
for char in S:
freqs[char] += 1
# 비교 없이 보석(J) 빈도 수 합산
for char in J:
count += freqs[char]
return count
중요 내용
- defaultdict를 사용하면 비교 없이 바로 딕셔너리를 생성할 수 있다.
풀이 3: counter로 계산 생략
class Solution:
def numJewelsInStones(self, J: str, S: str) -> int:
freqs = collections.Counter(S) # 돌(S) 빈도 수 계산
count = 0
# 비교 없이 보석(J) 빈도 수 합산
for char in J:
count += freqs[char]
return count
중요 내용
- defaultdict에 반복문을 써서 돌 문자열에 대한 딕셔너리를 직접 만드는 방법이 아닌 counter함수를 사용하여 단 한 줄로 만들 수 있었다.
풀이 4: 파이썬다운 방식
class Solution:
def numJewelsInStones(self, J: str, S: str) -> int:
return sum(s in J for s in S)
중요 내용
- 리스트 컴프리헨션을 이용한 반복문에 함수를 적용할 때는 괄호[]를 생략할 수 있다.
Question 30: 중복 문자 없는 가장 긴 부분 문자열 (재풀이)
중복 문자가 없는 가장 긴 부분 문자열의 길이를 리턴하라.
입력: s = “abcabcbb”
출력: 3
내 풀이
결국 풀지 못하였다.
풀이 1: 슬라이딩 윈도우오 투 포인터로 사이즈 조절
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
# 키가 char, 값이 value 가 되는 딕셔너리를 생성함
used = {}
max_length = start = 0
for index, char in enumerate(s):
# 이미 등장했던 문자라면 `start` 위치 갱신
if char in used and start <= used[char]:
start = used[char] + 1
else: # 최대 부분 문자열 길이 갱신
max_length = max(max_length, index - start + 1)
# 현재 문자의 위치 삽입
used[char] = index
return max_length
중요 내용
- 슬라이딩 윈도우를 옮기면서 이미 등장했던 문자라면 start 위치를 갱신하며 푸는 방식이다.
- 배열 챕터에 나왔던 슬라이딩 윈도우와 투 포인터를 응용한 방법이다.
Question 31: 상위 K 빈도 요소 (재풀이)
상위 k번 이상 등장하는 요소를 추출하라
입력: nums = [1,1,1,2,2,3], k = 2
출력: [1,2]
내 풀이
class Solution:
def topKFrequent(self, nums: List[int], k: int) -> List[int]:
nums_count = collections.Counter(nums)
return sorted(nums_count.keys(), key=lambda x:nums_count[x])[-k:]
- 이 문제는 상당히 쉽게 접근하였다.
- counter() 함수를 사용하여 각 숫자가 나타나는 횟수를 나타내는 딕셔너리를 만들었다.
- sorted() 에 람다 함수를 사용하여 숫자가 나타나는 횟수를 기준으로 숫자를 정렬하였다.
결과
Runtime: 145 ms, faster than 46.25% of Python3 online submissions for Top K Frequent Elements. Memory Usage: 18.6 MB, less than 90.78% of Python3 online submissions for Top K Frequent Elements.
풀이 1: 해시 테이블을 이용한 풀이
class Solution:
def topKFrequent(self, nums: List[int], k: int) -> List[int]:
freqs = collections.Counter(nums)
freqs_heap = []
for f in freqs:
heapq.heappush(freqs_heap, (-freqs[f], f))
topk = list()
for _ in range(k):
topk.append(heapq.heappop(freqs_heap)[1])
return topk
중요 내용
- 힙에 값을 삽입하는 방식은 다음과 같이 크게 두가지가 있다.
- 리스트를 만든 후 heapify()를 적용한다.
- 값을 삽입할 때 마다 매번 heappush()를 사용한다.
- 힙은 우선순위 큐를 구현할때 사용된다. 따라서 작은 값부터 차례로 정렬되서 값들이 저장되게 된다.
풀이 2: 파이썬다운 방식
class Solution:
def topKFrequent(self, nums: List[int], k: int) -> List[int]:
return list(zip(*collections.Counter(nums).most_common(k)))[0]
중요 내용
- zip() 함수는 2개 이상의 시퀀스를 일대일 대응하는 새로운 튜플 시퀀스로 만드는 역할을 한다.
- *은 시퀀스 언패킹 연산자로, 시퀀스를 풀어 해친다. 반대로 언패킹 된 시퀀스에 사용하면 다시 패킹할 수 있다.

Comments