최단 경로 문제
들어가기 전에
Dijkstra algorithm works as follows:
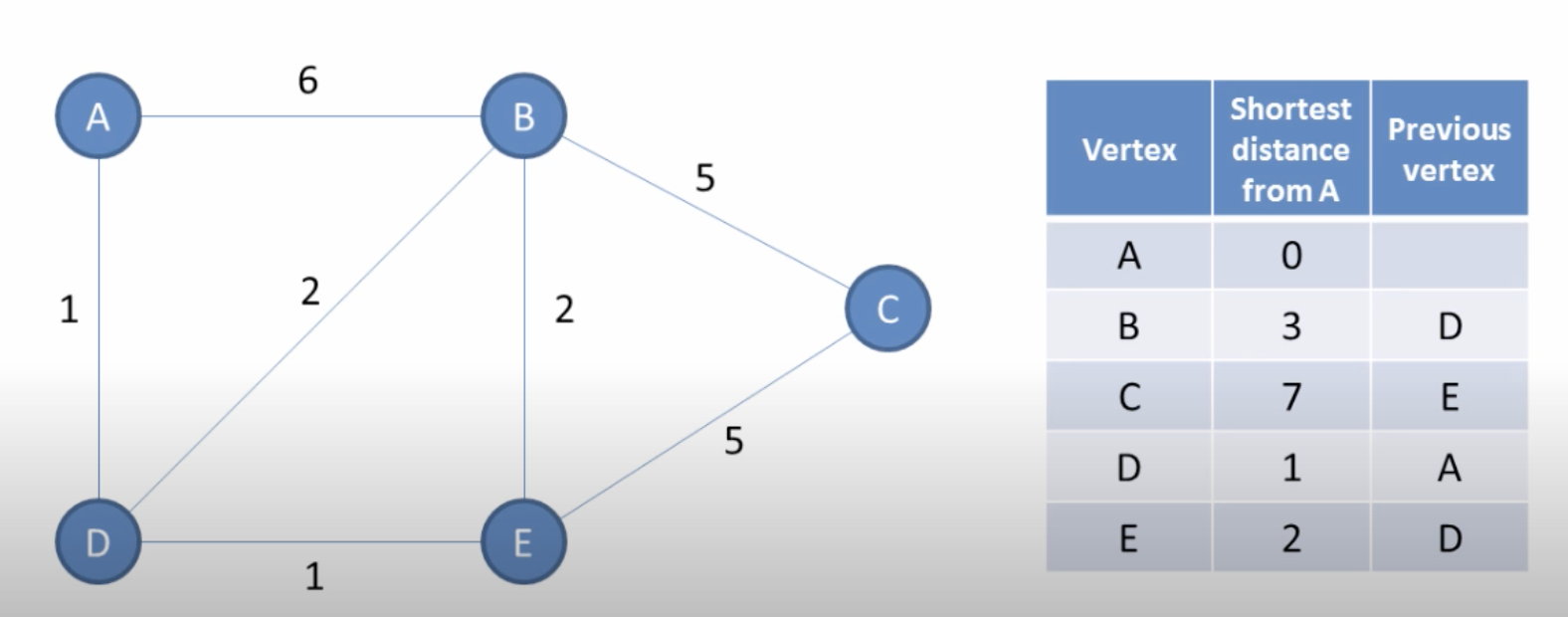
- Let distance of start vertex from start vertex to 0.
- Let all other vertices from start vertex to infinity.
- Visit the unvisited neighboring vertices of the start vertex.
- Update the shortest distance from A and previous vertex for the neighboring vertices
- Go to the nearest vertex and repeat the process of #2, #3.
- Clarify the unvisited vertices and visited vertices.
- When all vertices are visited, shortest distance from A can be defined.
Question 40: 네트워크 딜레이 타임
K부터 출발해 모든 노드가 신호를 받을 수 있는 시간을 계산하라. 불가능할 경우 -1를 리턴한다. 입력값 (u,v,w)는 각각 출발지, 도착지, 소요 시간으로 구성되며, 전체 노드의 개수는 N으로 입력받는다.
입력: times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
출력: 2
내 풀이
최단 경로 문제에 대한 걔념이 확실하게 잡혀있지 않은 상태에서 일단 풀이를 보류하였다.
풀이 1: 다익스트라 알고리즘 구현
class Solution:
def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
graph = collections.defaultdict(list)
for u, v, w in times:
graph[u].append((v, w))
# 큐 변수: [(소요시간), (정점)]
Q = [(0, k)]
dist = collections.defaultdict(int)
while Q:
time, node = heapq.heappop(Q)
# 주변에 방문하지 않은 정점을 방문함
if node not in dist:
dist[node] = time
for v, w in graph[node]:
alt = time + w
heapq.heappush(Q, (alt, v))
# 모든 경로를 방문하였는지 여부를 검사함
if len(dist) == n:
return max(dist.values())
return -1
중요 내용
- 다익스트라 알고리즘의 작동원리를 이해하면 위 코드도 이해하기 쉬울 것이다.
- 탐색한 육지가 섬일 경우 count를 1 증가시킨다.
- 이미 탐색한 육지일 경우 # (아무 문자나 가능하다)로 변경한다.
Question 41: K 경유지 내 가장 저렴한 항공권
시작점에서 도착점까지의 가장 저렴한 가격을 계산하되, k개의 경유지 이내에 도착하는 가격을 리턴하라. 경로가 존재하지 않을 경우 -1을 리턴한다.
입력: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1
출력: 200
내 풀이
풀지 못하였다.
풀이 1: 다익스트라 알고리즘 구현
class Solution:
def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:
# graph는 시작점과 종점, 시간을 나타내는 그림이라고 생각하면 됨
graph = collections.defaultdict(list)
for u, v, w in flights:
graph[u].append((v, w))
# Q는 (시작점에서 노드까지 걸린 시간, 노드, 남은 노드 수) 를 나타내는 큐이다.
Q = [(0, src, k)]
while Q:
price, node, remain = heapq.heappop(Q)
if node == dst:
return price
if remain >= 0:
for v, w in graph[node]:
alt = price + w
heapq.heappush(Q, (alt, v, remain-1))
return -1
중요 내용
- 40번 문제와 비슷하나 노드까지 걸린시간을 저장할 필요가 없으므로 dist변수는 삭제한다.
- 도착노드에 도달하면 반복문을 종료한다.
- 아직도 heapq를 사용하는 이유를 잘 모르겠다..
Question 34: 순열
서로 다른 정수를 입력받아 가능한 모든 순열을 리턴하라.
입력: [1,2,3]
출력: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
내 풀이
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
def dfs(permutations: List[int]):
if len(permutations) == len(nums):
results.append(permutations)
else:
for i in nums:
if i not in permutations:
next_p = permutations[:]
next_p.append(i)
dfs(next_p)
lst: List[int] = []
results = []
dfs(lst)
return results
- 문제 33번과 비슷한 dfs 방법으로 문제를 풀었다.
결과
Runtime: 67 ms, faster than 27.66% of Python3 online submissions for Permutations. Memory Usage: 14 MB, less than 95.52% of Python3 online submissions for Permutations.
풀이 1: DFS를 활용한 순열 생성
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
results = []
prev_elements = []
def dfs(elements):
# 리프 노드일때 결과 추가
if len(elements) == 0:
results.append(prev_elements[:])
# 순열 생성 재귀 호출
for e in elements:
next_elements = elements[:]
next_elements.remove(e)
prev_elements.append(e)
dfs(next_elements)
prev_elements.pop()
dfs(nums)
return results
중요 내용
- dfs 함수에 넣는 인수는 반드시 dfs의 인수와 이름이 동일해서는 안된다.
- results.append(prev_elements[:]) 에서 prev_elements 를 그대로 넣으면 prev_elements에 대한 참조가 추가되어 참조될 값이 변경될 경우 같이 바뀌게 된다.
풀이 2: itertools 모듈 사용
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
return list(map(list, itertools.permutations(nums)))
중요 내용
- itertools의 permutations 모듈을 사용하면 금방 풀이가 가능하다.
Question 35: 조합
전체 수 n을 입력받아 k개의 조합을 리턴하라
입력: n = 4, k = 2
출력: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]
내 풀이
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
def dfs(combs):
if len(combs) == k:
results.append(combs[:])
else:
if len(combs) == 0:
last_val = 1
else:
last_val = combs[-1]
for i in range(last_val,n+1):
if i not in combs:
next_combs = combs[:]
next_combs.append(i)
dfs(next_combs)
results = []
dfs([])
return results
- 순열을 생성하는 알고리즘과 거의 비슷한 코드로 작성하였다.
- 순열 알고리즘과 다른 점이라면 조합 배열의 마지막 요소를 별도로 지정하여서 그 요소가 반복문에서 최소값이 되도록 설정하였다.
결과
Runtime: 804 ms, faster than 14.34% of Python3 online submissions for Combinations. Memory Usage: 15.9 MB, less than 42.85% of Python3 online submissions for Combinations.
풀이 1: DFS로 k개 조합 생성
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
results = []
def dfs(elements, start: int, k: int):
if k == 0:
results.append(elements[:])
return
# 자신 이전의 모든 값을 고정하여 재귀 호출
for i in range(start, n + 1):
elements.append(i)
dfs(elements, i + 1, k - 1)
elements.pop()
dfs([], 1, k)
return results
중요 내용
- 내 풀이 방법과 비슷하나 여기서는 반복문의 시작하는 값을 dfs 인수로 설정할 수 있게 하였다.
- 재귀 구조를 돌고 나서 조합 요소의 마지막 값을 삭제함으로써 그 전에 값을 복사하는 과정을 생략하였다. 이렇게 하는 것과 값을 복사했을때의 실행 시간은 비슷하여 어느 방법을 사용해도 무방할 것 같다.
풀이 2: 파이썬다운 방식
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
return list(itertools.combinations(range(1, n+1), k))
중요 내용
- 순열 문제와는 달리 조합 문제의 경우 DFS와 모듈 사이의 성능 차이가 꽤 큰 편이다.
Question 36: 조합
숫자 집합 candidated를 조합하여 합이 target이 되는 원소를 나열하라. 각 원소는 중복으로 나열 가능하다.
입력: candidates = [2,3,6,7], target = 7
출력: [[2,2,3],[7]]
내 풀이
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
def dfs(start, subset):
if len(subset) <= len(nums):
results.append(subset[:])
for idx in range(start, len(nums)):
if nums[idx] not in subset:
subset.append(nums[idx])
dfs(idx+1, subset)
subset.pop()
results = []
dfs(0,[])
return results
- DFS 방법으로 풀었다.
- 반복문의 최솟값을 지정함으로써 순열이 아닌 조합으로 문제에 접근하였다.
- 조합 풀이 방법을 그대로 이용하였으나 부분집합의 요소 수가 전체 요소의 수보다 적으면 결과 리스트에 append 하도록 하였다.
결과
Runtime: 32 ms, faster than 92.62% of Python3 online submissions for Subsets. Memory Usage: 14.2 MB, less than 63.33% of Python3 online submissions for Subsets.
풀이 1: 트리의 모든 DFS 결과
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
result = []
def dfs(index, path):
# 매 번 결과 추가
result.append(path)
# 경로를 만들면서 DFS
for i in range(index, len(nums)):
dfs(i + 1, path + [nums[i]])
dfs(0, [])
return result
중요 내용
- path의 합이 target보다 크면 반복문을 종료하는 과정은 내 풀이 방법과 동일하다.
- 여기서는 타겟값을 dfs 함수에 인수로 전달하며 candidates의 원소값을 하나씩 빼가며 탐색하는 방법으로 작동한다.
Question 37: 부분 집합
모든 부분 집합을 리턴하라
입력: nums = [1,2,3]
출력: [[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
내 풀이
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
def dfs(start, subset):
if len(subset) <= len(nums):
results.append(subset[:])
for idx in range(start, len(nums)):
if nums[idx] not in subset:
subset_copy = subset[:]
subset_copy.append(nums[idx])
dfs(idx+1, subset_copy)
results = []
dfs(0,[])
return results
- DFS 방법으로 풀었다.
- 반복문의 최솟값을 지정함으로써 순열이 아닌 조합으로 문제에 접근하였다.
결과
Runtime: 163 ms, faster than 22.06% of Python3 online submissions for Combination Sum. Memory Usage: 14.1 MB, less than 76.76% of Python3 online submissions for Combination Sum.
풀이 1: 트리의 모든 DFS 결과
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
result = []
def dfs(index, path):
# 매 번 결과 추가
result.append(path)
# 경로를 만들면서 DFS
for i in range(index, len(nums)):
dfs(i + 1, path + [nums[i]])
dfs(0, [])
return result
중요 내용
- range에서 지정한 시작 값이 끝 값보다 큰 경우 해당 반복문을 실행하지 않는다.
- 여기서 result.append()에 path[:]가 아닌 그냥 path를 넣어도 실행되는 이유를 잘 모르겠다. path+[nums[i]]를 하며 path에 새로운 값에 대한 참조가 아닌 새로운 값이 생성되어 그런 것이라는 추측만 할 수 있었다.
Question 38: 일정 재구성
[from, to]로 구성된 항공권 목록을 이용해 JFK에서 출발하는 여행 일정을 구성하라. 여러 일정이 있는 경우 사전식 순서로 방문한다.
입력: [[“JFK”,”SFO”],[“JFK”,”ATL”],[“SFO”,”ATL”],[“ATL”,”JFK”],[“ATL”,”SFO”]]
출력: [“JFK”,”ATL”,”JFK”,”SFO”,”ATL”,”SFO”]
내 풀이
class Solution:
def findItinerary(self, tickets: List[List[str]]) -> List[str]:
def dfs(results, next_ticket):
if len(results)-1 == len(tickets):
candidates.append(results[:])
else:
last_ticket = results[-1]
for idx in range(len(next_ticket)):
if last_ticket == next_ticket[idx][0]:
results.append(next_ticket[idx][1])
tickets_copy_copy = next_ticket[:]
del tickets_copy_copy[idx]
dfs(results, tickets_copy_copy)
results.pop()
def sort_func(x):
start_letter = ''
for i in x:
start_letter += i[0]
return start_letter
candidates = []
for ticket in tickets:
if ticket[0] == 'JFK':
init_result = ticket
tickets_copy = tickets[:]
tickets_copy.remove(ticket)
dfs(init_result, tickets_copy)
candidates.sort(key = sort_func)
return candidates[0]
- DFS 방법으로 풀었다.
- ticket으로 가능한 여행 경로를 모두 후보 리스트에 넣고 후보 리스트를 사전식 순서로 정렬하였다.
결과
특정 값을 넣을때 올바른 답을 출력하지 않는 오류가 발생하였다.
풀이 1: DFS로 일정 그래프 구성
class Solution:
def findItinerary(self, tickets: List[List[str]]) -> List[str]:
graph = collections.defaultdict(list)
# 그래프 순서대로 구성
for a, b in sorted(tickets):
graph[a].append(b)
route = []
def dfs(a):
# 첫 번째 값을 읽어 어휘순 방문
while graph[a]:
dfs(graph[a].pop(0))
route.append(a)
dfs('JFK')
# 다시 뒤집어 어휘순 결과로
return route[::-1]
중요 내용
- 내가 풀이한 방법과는 매우 다르게 defaultdict 함수를 사용하여 간단하게 풀이하였다.
- sorted를 nested list에 사용하면 nested list 안의 요소를 기준으로 정렬한다.
풀이 2: 스택 연산으로 큐 연산 최적화 시도
class Solution:
def findItinerary(self, tickets: List[List[str]]) -> List[str]:
graph = collections.defaultdict(list)
# 그래프 뒤집어서 구성
for a, b in sorted(tickets, reverse=True):
graph[a].append(b)
route = []
def dfs(a):
# 마지막 값을 읽어 어휘순 방문
while graph[a]:
dfs(graph[a].pop())
route.append(a)
dfs('JFK')
# 다시 뒤집어 어휘순 결과로
return route[::-1]
중요 내용
- pop() 함수는 시간 복잡도가 O(1) 인 반면 pop(0)은 시간 복잡도가 O(n) 이다. 따라서 스택 방법으로 푸는 것이 훨씬 더 효과적이다.
- 티켓을 정렬할 때 reverse=True 로 설정하여서 내림차순으로 정렬되게 하였다.
풀이 3: 일정 그래프 반복
class Solution:
def findItinerary(self, tickets: List[List[str]]) -> List[str]:
graph = collections.defaultdict(list)
for a,b in sorted(tickets):
graph[a].append(b)
route, stack = [], ['JFK']
while stack:
while graph[stack[-1]]:
stack.append(graph[stack[-1]].pop(0))
route.append(stack.pop())
return route[::-1]
중요 내용
- 스택을 이용한 반복으로 처리를 하였다.
- route는 더 이상 진행할 경로가 없을 때를 위해서 만든 리스트이다.
Question 39: 코스 스케줄
0을 완료하기 위해서는 1을 끝내야 한다는 것을 [0,1] 쌍으로 표현하는 n개의 코스가 있다. 코스 개수 n과 이 쌍들을 입력으로 받았을 때 모든 코스가 완료 가능한지 판별하라.
입력: numCourses = 2, prerequisites = [[1,0],[0,1]]
출력: False
- 순환 구조가 되면 false를 리턴한다.
내 풀이
- 순환 구조를 판별하는 부분에서 계속 에러가 떠서 결국 풀지 못하였다.
풀이 1: DFS로 일정 그래프 구성
class Solution:
def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:
graph = collections.defaultdict(list)
# 그래프 구성
for x, y in prerequisites:
graph[x].append(y)
traced = set()
def dfs(i):
# 순환 구조이면 False
if i in traced:
return False
traced.add(i)
for y in graph[i]:
# 최종 결과를 False로 리턴하게 함
if not dfs(y):
return False
# 탐색 종료 후 순환 노드 삭제
traced.remove(i)
return True
# 노드를 하나씩 반복하며 순환 구조 판별
for x in list(graph):
# 최종 결과를 False로 리턴하게 함
if not dfs(x):
return False
return True
중요 내용
- defaultdict() 함수로 시작점과 종점의 위치를 나타내는 딕셔너리를 만든다.
- 노드를 하나씩 순환하며 순환 구조인지 판별한다.
- 판별이 끝나면 반드시 판별 여부를 검사하는 세트 변수를 초기화 시켜준다.
- 이렇게 실행했을때 불필요하게 동일한 그래프를 여러번 탐색하게 되므로 타임 에러가 뜬다.
- graph는 defaultdict이므로 반복문을 돌때마다 에러가 나지 않기 위해 값을 계속 추가해 나간다. 따라서 이러한 에러가 나지 않도록 리스트 형태로 만들어줘야 한다.
풀이 2: 가지치기를 이용한 최적화
class Solution:
def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:
graph = collections.defaultdict(list)
# 그래프 구성
for x, y in prerequisites:
graph[x].append(y)
traced = set()
visited = set()
def dfs(i):
# 순환 구조이면 False
if i in traced:
return False
# 이미 방문했던 노드이면 True
if i in visited:
return True
traced.add(i)
for y in graph[i]:
if not dfs(y):
return False
# 탐색 종료 후 순환 노드 삭제
traced.remove(i)
# 탐색 종료 후 방문 노드 추가
visited.add(i)
return True
# 순환 구조 판별
for x in list(graph):
if not dfs(x):
return False
return True
중요 내용
- visited 변수에 이미 방문했던 노드면 스킵할 수 있도록 한 번 방문했던 노드를 저장한다.
- 이렇게 가지치기를 하면 실행시간이 훨씬 더 단축되어 타임에러가 뜨지 않는다.

Comments