트리 - part1
들어가기 전에
이진 트리의 유형은 다음과 같다.
- 정 이진 트리(Full Binary Tree): 모든 노드가 0개 또는 2개의 자식 노드를 갖는다.
- 완전 이진 트리(Complete Binary Tree): 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있으며, 마지막 레벨의 모든 노드는 가장 왼쪽부터 채워져 있다.
- 포화 이진 트리(Perfect Binary Tree): 모든 노드가 2개의 자식 노드를 갖고 있으며, 모든 리프 노드가 동일한 깊이 또는 레벨을 갖는다.
Question 42: 이진 트리의 최대 깊이
이진 트리의 최대 깊이를 구하여라
입력: [3,9,20,null,null,15,7]
출력: 3
내 풀이
이진 트리에 대한 걔념이 확실하게 잡혀있지 않은 상태에서 일단 풀이를 보류하였다.
풀이 1: 반복 구조로 BFS 풀이
class Solution:
def maxDepth(self, root: TreeNode) -> int:
if root is None:
return 0
queue = collections.deque([root])
depth = 0
while queue:
depth += 1
# 큐 연산 추출 노드의 자식 노드 삽입
for _ in range(len(queue)):
cur_root = queue.popleft()
if cur_root.left:
queue.append(cur_root.left)
if cur_root.right:
queue.append(cur_root.right)
# BFS 반복 횟수 == 깊이
return depth
중요 내용
- TreeNode 라는 별도의 클래스를 만들었다. left는 왼쪽에 위치한 자식노드, right는 오른쪽에 위치한 자식노드이다.
- 트리를 데크형으로 선언하여 풀이 속도를 높였다.
- 큐 방법을 이용하여 푸는 것은 BFS 방법이다
Question 43: 이진 트리의 직경
이진 트리에서 두 노드 간 가장 긴 경로의 길이를 출력하라.
입력: [1,2,3,4,5]
출력: 3
내 풀이
풀지 못하였다.
풀이 1: 상태값 누적 트리 DFS
class Solution:
longest = 0
def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
def dfs(node: TreeNode) -> int:
if not node:
return -1
left = dfs(node.left)
right = dfs(node.right)
self.longest = max(self.longest, left+right+2)
return max(left, right) + 1
dfs(root)
return self.longest
중요 내용
- 여기서 상태값이라는 개념이 나오는데, 노드가 가지고 있는 실질적인 숫자값을 의미한다.
- 자식 노드가 없으면 -1을 리턴하므로 거리, 상태값 모두 0이 된다.
- 트리는 같은 depth에 존재하는 노드끼리 묶어서 생각하는 것이 편하다.
- 재귀함수를 이용하여 푸는 것은 DFS 이다.
- root: Optional[TreeNode]는 node: TreeNode 와 같다.
Question 44: 가장 긴 동일 값의 경로
동일한 값을 지닌 가장 긴 경로를 찾아라.
입력: root = [5,4,5,1,1,5]
출력: 2
풀이 1: 상태값 거리 계산 DFS
class Solution:
result: int = 0
def longestUnivaluePath(self, root: Optional[TreeNode]) -> int:
def dfs(node: TreeNode) -> int:
if not node:
return 0
left = dfs(node.left)
right = dfs(node.right)
if node.left and node.left.val == node.val:
left += 1
else:
left = 0
if node.right and node.right.val == node.val:
right += 1
else:
right = 0
# 왼쪽과 오른쪽 자식 노드 간 거리의 합 최댓값이 결과
self.result = max(self.result, left+right)
# 자식 노드 상태값 중 큰 값 리턴 (가장 긴 경로를 찾아야 하므로)
return max(left, right)
dfs(root)
return self.result
중요 내용
- 여기서는 리프 노드에 위치한 상태값은 0이 된다.
- 만약 왼쪽 아래나 오른쪽 아래 노드가 현재 노드와 같으면 1을 리턴한다.
- 트리의 직경이나 경로를 찾는 문제는 상태값을 이용해 접근해야 한다!
결과
Runtime: 404 ms, faster than 76.45% of Python3 online submissions for Longest Univalue Path. Memory Usage: 17.8 MB, less than 81.53% of Python3 online submissions for Longest Univalue Path.
Question 45: 이진 트리 반전
이진 트리를 반전시켜라
입력: root = [4,2,7,1,3,6,9]
출력: [4,7,2,9,6,3,1]
내 풀이
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
def dfs(node: TreeNode):
if not node:
return
left = node.left
node.left = node.right
node.right = left
dfs(node.left)
dfs(node.right)
dfs(root)
return root
- dfs방법을 이용하여 재귀함수로 풀었다.
결과
Runtime: 48 ms, faster than 39.27% of Python3 online submissions for Invert Binary Tree. Memory Usage: 13.9 MB, less than 83.62% of Python3 online submissions for Invert Binary Tree.
풀이 1: 파이썬다운 방식
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if root:
root.left, root.right = self.invertTree(root.right), self.invertTree(root.left)
return root
중요 내용
- 마찬가지로 재귀 구조로 풀었다.
- 제일 리프노드에 위치한 숫자끼리 반전된다.
풀이 2: 반복 구조로 BFS
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
queue = collections.deque([root])
while queue:
node = queue.popleft()
if node:
node.left, node.right = node.right, node.left
queue.append(node.left)
queue.append(node.right)
return root
중요 내용
- 부모 노드부터 스왑하면서 계속 아래로 내려가는 하향식 방법이다.
풀이 3: 반복 구조로 DFS
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
stack = collections.deque([root])
while stack:
node = stack.pop()
if node:
node.left, node.right = node.right, node.left
stack.append(node.left)
stack.append(node.right)
return root
중요 내용
- 앞에 queue.popleft()을 stack.pop() 으로 바꾸는 것 만으로 DFS 방법으로 변경하였다.
풀이 4: 반복 구조로 DFS 후위 순회
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
stack = collections.deque([root])
while stack:
node = stack.pop()
if node:
stack.append(node.left)
stack.append(node.right)
node.left, node.right = node.right, node.left
return root
중요 내용
- 앞선 풀이는 전위 순회 형태로 처리한 반면 해당 풀이 방법은 후위 순회로 변경하였다.
Question 46: 두 이진 트리 병합
두 이진 트리를 병합하라. 중복되는 노드는 값을 합산한다.
입력: root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
출력: [3,4,5,5,4,null,7]
내 풀이
- 새로운 TreeNode를 생성하는 법을 몰랐기 때문에 결국 풀지 못하였다.
풀이 1: 재귀 탐색
class Solution:
def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:
if root1 and root2:
node = TreeNode(root1.val + root2.val)
node.left = self.mergeTrees(root1.left, root2.left)
node.right = self.mergeTrees(root1.right, root2.right)
return node
# 노드의 left또는 right값이 없으면 둘 중 값이 있는 한개의 노드만 리턴함
else:
return root1 or root2
중요 내용
- 트리구조를 이루는 노드를 생성하는 함수는 TreeNode이다.
- DFS 방법으로 풀었다.
Question 47: 이진 트리 직렬화 & 역직렬화
이진트리를 배열로 직렬화 하고, 반대로 역질렬화하는 기능을 구현하라.
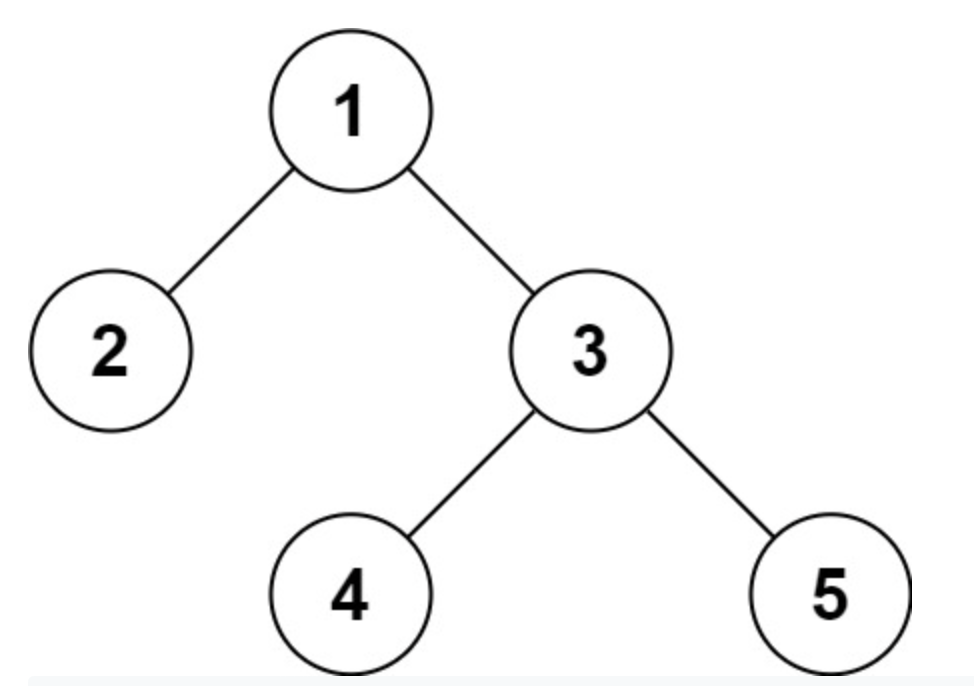
입력: root = [1,2,3,null,null,4,5]
출력: [1,2,3,null,null,4,5]
풀이 1: 직렬화 & 역직렬화 구현
class Codec:
def serialize(self, root):
queue = collections.deque([root])
result = ['#']
while queue:
node = queue.popleft()
if node:
queue.append(node.left)
queue.append(node.right)
result.append(str(node.val))
else:
result.append('#')
return ''.join(result)
def deserialize(self, data: str) -> TreeNode:
# 예외 처리
if data == '# #':
return None
print(data)
root = TreeNode(int(data[1]))
queue = collections.deque([root])
index = 2
# 빠른 런너처럼 자식 노드 결과 먼저 확인 후 큐 삽입
while queue:
node = queue.popleft()
if data[index] is not '#':
node.left = TreeNode(int(data[index]))
queue.append(node.left)
index += 1
if data[index] is not '#':
node.right = TreeNode(int(data[index]))
queue.append(node.right)
index += 1
return root
중요 내용
- BFS 방법으로 구현하였다.
- 이진 트리는 논리적인 데이터 구조인데, 이를 파일이나 디스크에 저장하기 위해 물리적인 형태로 바꾸는 것을 직렬화(seralize) 라고 한다.
- null을 #으로 표현이 가능하다.
- 부모와 자식 노드의 위치는 각각 부모 [i/2], 왼쪽 자식 2i, 오른쪽 자식 2i+1의 수식으로 계산할 수 있다. 이 방법은 역직렬화 할때 사용되었다.
Question 48: 균형 이진 트리
이진 트리가 높이 균형인지 판단하라. 높이 균형은 모든 노드의 서브 트리 간의 높이 차이가 1 이하인 것을 말한다.
입력: root = [3,9,20,null,null,15,7]
출력: true
내 풀이
풀지 못하였다.
풀이 1: 재귀 구조로 높이 차이 계산
class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
def check(root):
if not root:
return 0
left = check(root.left)
right = check(root.right)
# 만약 노드의 상태값끼리의 차이가 1보다 크거나 노드의 크기가 -1 이면 계속 -1을 리턴한다.
if left == -1 or right == -1 or abs(left-right) > 1:
return -1
return max(left, right) + 1
return check(root) != -1
중요 내용
- 재귀 함수를 이용해 DFS 방법으로 풀었다.
- 노드의 상태값끼리의 차이의 절대값이 1보다 크거나 노드의 크기가 -1 이면 계속 -1을 리턴한다.
Question 49: 최소 높이 트리
노드 개수와 무방향 그래프를 입력받아 트리가 최소 높이가 되는 루트의 목록을 리턴하라.
입력: n = 4, edges = [[1,0],[1,2],[1,3]]
출력: [1]
내 풀이
풀지 못하였다.
풀이 1: 단계별 리프 노드 제거
class Solution:
def findMinHeightTrees(self, n: int, edges: List[List[int]]) -> List[int]:
if n <= 1:
return [0]
graph = collections.defaultdict(list)
for i,j in edges:
graph[i].append(j)
graph[j].append(i)
leaves = []
for i in range(n+1):
if len(graph[i]) == 1:
leaves.append(i)
while n > 2:
n -= len(leaves)
new_leaves = []
for leaf in leaves:
neighbor = graph[leaf].pop()
graph[neighbor].remove(leaf)
if len(graph[neighbor]) == 1:
new_leaves.append(neighbor)
print(leaves)
leaves = new_leaves
return leaves
중요 내용
- 이 문제에서의 트리는 일반 이진트리와는 다르게 접근해야한다.
- 최소 높이를 구성하려면 가운데에 있는 값이 루트여야 한다.
- 각 노드를 key, 그 노드의 도착점을 value 로 하여 딕셔너리를 구성하였을때 리프 노드는 딕셔너리에서 해당 키의 값이 1개 뿐인 것을 말한다.
- 리프 노드에서부터 차례로 근접한 노드를 찾아가며 키의 값이 1개뿐인 리프 노드를 찾아 나간다.

Comments