트리 - part2
들어가기 전에
이진 탐색 트리(BST)란?
이진 탐색 트리란 노드의 왼쪽 서브트리에는 그 노드의 값보다 작은 값들을 지닌 노드로 이루어진 반면, 오른쪽 서브트리는 그 노드의 값보다 큰 값들을 지닌 노드로 이루어져 있는 트리이다. 탐색시 시간 복잡도가 O(log n) 이다.
자가 균형 이진 탐색 트리
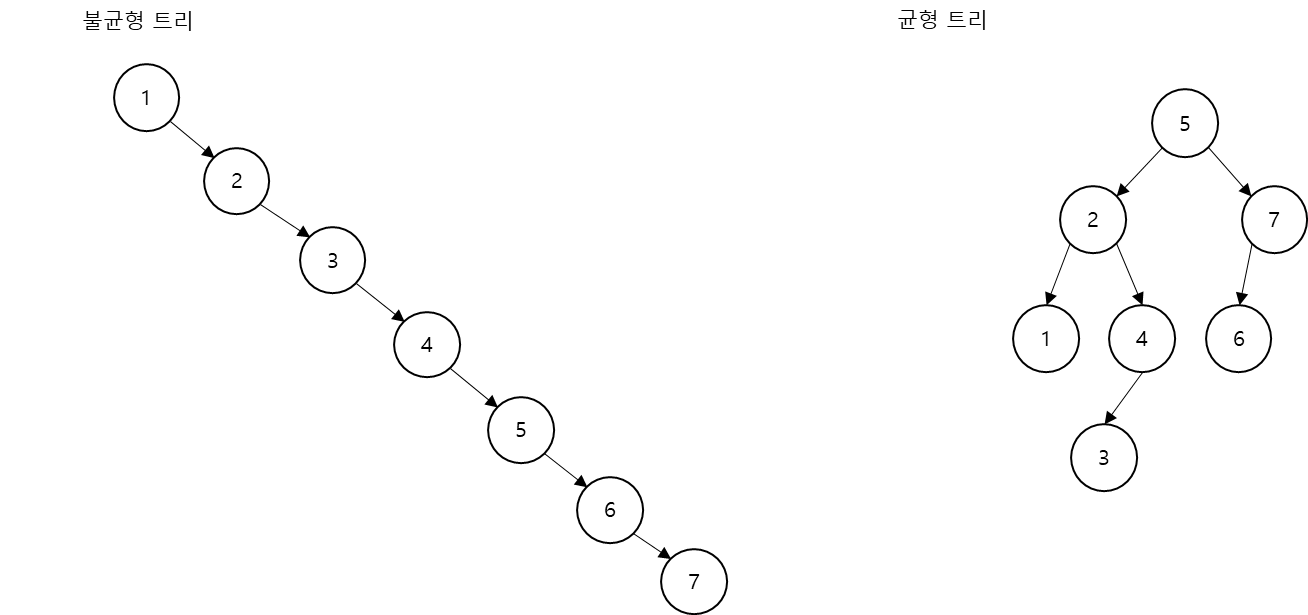
일반 이진 트리는 운이 나쁘면 로그 계산을 기반으로 하는 이진 탐색 트리의 장점을 전혀 살릴 수 없다. 자가 균형 이진 탐색 트리는 이러한 문제점을 해결하기 위해 고안된 탐색 방법으로, 아래 모습과 같이 효율적으로 탐색이 가능해진다.
Question 50: 정렬된 배열을 높이 균형 이진 탐색 트리 변환
오름차순으로 정렬된 배열을 높이 균형 이진 탐색 트리로 변환하여라
입력: nums = [-10,-3,0,5,9]
출력: [0,-3,9,-10,null,5]
내 풀이
이진 탐색 트리에 대한 걔념이 확실하게 잡혀있지 않은 상태에서 일단 풀이를 보류하였다.
풀이 1: 반복 구조로 BFS 풀이
class Solution:
def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:
if not nums:
return None
mid = len(nums) // 2
node = TreeNode(nums[mid])
node.left = self.sortedArrayToBST(nums[:mid])
node.right = self.sortedArrayToBST(nums[mid+1:])
return node
중요 내용
- 중앙값을 노드로 설정하여 재귀구조를 이용해 풀었다.
Question 51: 이진 탐색 트리를 더 큰 수 합계 트리로
BST의 각 노드를 현재값보다 더 큰 값을 가진 모든 노드의 합으로 만들어라
입력: root = [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
출력: [30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
내 풀이
class Solution:
def bstToGst(self, root: TreeNode) -> TreeNode:
deque = collections.deque([root])
node_list = []
while deque:
node = deque.popleft()
node_list.append(node.val)
if node.left:
deque.append(node.left)
if node.right:
deque.append(node.right)
deque2 = collections.deque([root])
while deque2:
node = deque2.popleft()
bigger_val = sum([i for i in node_list if i>=node.val])
node.val = bigger_val
if node.left:
deque2.append(node.left)
if node.right:
deque2.append(node.right)
return root
- BFS 방법으로 이진트리의 값을 node_list에 모두 저장한뒤 다시 BFS 방법을 이용하여 노드의 값을 자기보다 큰 값의 합으로 변경하였다.
풀이 1: 중위 순회로 노드 값 누적
class Solution:
val: int = 0
def bstToGst(self, root: TreeNode) -> TreeNode:
if root:
self.bstToGst(root.right)
self.val += root.val
root.val = self.val
self.bstToGst(root.left)
return root
중요 내용
- 자신보다 크거나 같은 값을 찾기 위해서는 자신을 포함한 우측 자식 노드의 합을 구하면 된다.
- 우측 -> 부모 -> 좌측 순서로 이동하면서 자신의 값을 포함해 누적값을 구한다.
Question 52: 이진 탐색 트리(BST) 합의 범위
이진탐색트리가 주어졌을 떄 L이상 R 이하의 값을 지닌 노드의 합을 구하라.
입력: root = [10,5,15,3,7,null,18], low = 7, high = 15
출력: 32
내 풀이
class Solution:
def rangeSumBST(self, root: Optional[TreeNode], low: int, high: int) -> int:
total = 0
queue = collections.deque([root])
while queue:
node = queue.popleft()
if node.val >= low and node.val <= high:
total += node.val
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return total
- BFS 방법으로 노드를 하나씩 최솟값과 최댓값과 비교해가며 사이에 있으면 전체 합에 추가시키는 방식으로 풀었다.
풀이 결과
Runtime: 318 ms, faster than 48.54% of Python3 online submissions for Range Sum of BST. Memory Usage: 23.4 MB, less than 5.11% of Python3 online submissions for Range Sum of BST.
풀이 1: 재귀 구조 DFS로 브루트 포스 탐색
class Solution:
def rangeSumBST(self, root: TreeNode, L: int, R: int) -> int:
if not root:
return 0
return (root.val if L <= root.val <= R else 0) + \
self.rangeSumBST(root.left, L, R) + \
self.rangeSumBST(root.right, L, R)
중요 내용
- 브루트 포스 방법으로 모든 노드가 L과 R범위 안에 포함되는지 여부를 확인한다.
- 모든 노드를 확인하므로 시간이 오래 걸린다.
풀이 2: DFS 가지치기로 필요한 노드 탐색
class Solution:
def rangeSumBST(self, root: TreeNode, L: int, R: int) -> int:
def dfs(node: TreeNode):
if not node:
return 0
if node.val < L:
return dfs(node.right)
elif node.val > R:
return dfs(node.left)
return node.val + dfs(node.left) + dfs(node.right)
return dfs(root)
중요 내용
- 왼쪽 노드는 항상 작고, 오른쪽 노드는 항상 크므로 최솟값보다 노드가 작으면 왼쪽 노드를 검사할 필요가 없고 최댓값보다 노드가 크면 오른쪽 노드를 검사할 필요가 없다.
- 따라서 조건문과 재귀구조를 이용해 dfs방법으로 풀이하였다.
풀이 3: 반복 구조 DFS로 필요한 노드 탐색
class Solution:
def rangeSumBST(self, root: Optional[TreeNode], low: int, high: int) -> int:
stack, sum = [root], 0
while stack:
node = stack.pop()
if node:
if node.val > low:
stack.append(node.left)
if node.val < high:
stack.append(node.right)
if low <= node.val <= right:
sum += node.val
return sum
중요 내용
- 이 풀이방법은 내가 풀이한 방법과 비슷하다.
- pop() 함수를 사용하면 DFS 방법이다.
풀이 4: 반복 구조 BFS로 필요한 노드 탐색
class Solution:
def rangeSumBST(self, root: Optional[TreeNode], low: int, high: int) -> int:
stack, sum = [root], 0
while stack:
node = stack.pop(0)
if node:
if node.val > low:
stack.append(node.left)
if node.val < high:
stack.append(node.right)
if low <= node.val <= high:
sum += node.val
return sum
중요 내용
- pop(0) 또는 popleft() 함수를 사용하면 BFS 방법이다.
Question 53: 이진 탐색 트리 노드 간 최소 거리
두 노드 간 값의 차이가 가장 작은 노드의 값의 차이를 출력하라
입력: root = [4,2,6,1,3,null,null]
출력: 1
내 풀이
class Solution:
def minDiffInBST(self, root: Optional[TreeNode]) -> int:
min_val = sys.maxsize
queue = collections.deque([root])
while queue:
node = queue.popleft()
if node.left:
queue.append(node.left)
min_val = min(min_val, node.val - node.left.val)
if node.right:
queue.append(node.right)
min_val = min(min_val, node.right.val - node.val)
return min_val
- 모든 경우의 수를 생각하지 않아 결국 풀지 못했다.
풀이 1: 재귀 구조로 중위 순회
class Solution:
prev = -sys.maxsize
result = sys.maxsize
def minDiffInBST(self, root: Optional[TreeNode]) -> int:
if root.left:
self.minDiffInBST(root.left)
self.result = min(self.result, root.val - self.prev)
self.prev = root.val
if root.right:
self.minDiffInBST(root.right)
return self.result
중요 내용
- 다음과 같은 과정으로 계산 과정이 이루어진다.
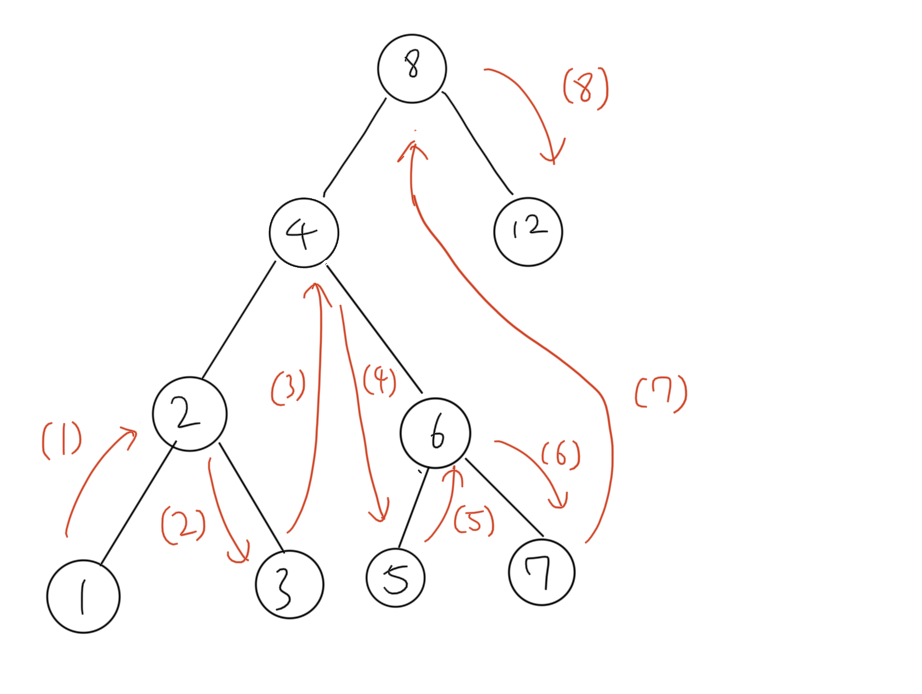
2. 여기서는 재귀구조로 중위 순회하는 방법으로 풀었다.
풀이 2: 반복 구조로 중위 순회
class Solution:
def minDiffInBST(self, root: Optional[TreeNode]) -> int:
prev = -sys.maxsize
result = sys.maxsize
stack = []
node = root
while stack or node:
while node:
stack.append(node)
node = node.left
node = stack.pop()
result = min(result, node.val - prev)
prev = node.val
print(node.val)
node = node.right
return result
중요 내용
- 풀이 1과 과정은 같으나 재귀구조가 아닌 while문을 사용한 반복 구조로 문제를 풀었다.
트리 순회
-
트리 순회: 그래프 순회의 한 형태로써 트리 자료구조에서 각 노드를 정확히 한번 방문하는 과정을 말한다.
- 트리 순회는 노드의 방문 순서에 따라 다음과 같이 3가지 방식으로 구분된다.
- 전위 순회: N -> L -> R
- 중위 순회: L -> N -> R
- 후위 순회: L -> R -> N
- 트리 순회는 재귀 구현이 훨씬 더 간단하고 직관적이다.
예제
[F, B, G, A, D, null, I, null, null, C, E, H, null] 에 각각의 트리 순회를 적용하였을 때 결과이다.
- 전위 순회
def preorder(node):
if node is None:
return
print(node.val)
preorder(node.left)
preorder(node.right)
preorder(root)
F, B, A, D, C, E, G, I, H
2. 중위 순회
def preorder(node):
if node is None:
return
preorder(node.left)
print(node.val)
preorder(node.right)
preorder(root)
A, B, C, D, E, F, G, H, I
3. 후위 순회
def preorder(node):
if node is None:
return
preorder(node.left)
preorder(node.right)
print(node.val)
preorder(root)
A, C, E, D, B, H, I, G, F
- print()의 위치만 잘 기억하면 전위/ 중위/ 후위를 잘 구분할 수 있을 것이다.
Question 54: 전위, 중위 순회 결과로 이진 트리 구축
트리의 전위, 중위 순회 결과를 입력값을 받아 이진 트리를 구축하라.
입력: 전위: [3,9,20,15,7] 후위: [9,3,15,20,7]
출력: [3,9,20,null,null,15,7]
내 풀이
- 전위와 중위의 연관성을 찾지 못해 한가지 입력값만 사용하여 풀려고 했으나 풀리지 않았다.
풀이 1: 전위 순회 결과로 중위 순회 분할 정복
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
if inorder:
index = inorder.index(preorder.pop(0))
node = TreeNode(inorder[index])
node.left = self.buildTree(preorder, inorder[:index])
node.right = self.buildTree(preorder, inorder[index+1:])
return node
중요 내용
- 전위 순회의 결과로 중위 순회를 인덱싱하여 분할시킨 값을 재귀 호출하며 풀었다.
- 전위 순회의 결과는 중위 순회 결과를 왼쪽과 오른쪽으로 분할시키는 역할을 한다.

Comments