배열
Question 7: 두 수의 합
입력: ‘num = [2,7,11,15], target = 9’
출력: [0,1]
내 풀이
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
for i in range(len(nums)):
for j in range(len(nums)):
if nums[i]+nums[j] == target and i!=j:
return [i,j]
결과
시간 초과 에러가 떴다.
에러 이유
1부터 n까지의 값을 가진 리스트가 있다고 하자. i와 j는 0에서부터 n까지의 값을 가져 $O(n^2)$ 만큼의 실행시간이 걸린다. 그러나 nums[1]+nums[2] 가 타겟 값이 아닐 때 nums[2]+nums[1]는 검사할 필요가 없다. 따라서 위 코드는 불필요한 계산과정까지 수반하므로 코드 실행 시간이 길어지게 되어 시간 초과 에러가 난다.
풀이 1: 브루트 포스로 계산
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
for i in range(len(nums)):
for j in range(i+1, len(nums)):
if nums[i]+nums[j] == target:
return [i,j]
중요 내용
- 브루트 포스는 배열을 반복하면서 모든 조합을 더해서 일일이 확인해보는 방법이다.
- 두번째 반복문에 시작값 i+1를 지정하여 불필요한 계산과정을 생략하였다.
- 브루트 포스는 반복문이 m개 있을 때 $O(n^m)$ 만큼 걸리므로 시간 초과 에러가 뜰 수 있으므로 좋은 방법은 아니다!
풀이 2: in을 이용한 탐색
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
for i,n in enumerate(nums):
complement = target-n
if complement in nums[i+1:]:
return[nums.index(n), nums[i+1:].index(complement)+(i+1)]
기억해야 할 함수
- list.index(찾을 값): 리스트에서 찾을 값의 인덱스를 리턴한다.
중요 내용
- 파이썬의 내부 함수로 구현된 in (풀이2)은 파이썬 레벨에서 매번 값을 비교하는 것(풀이1)에 비해 훨씬더 빨리 실행된다.
풀이 3: 첫 번째 수를 뺀 결과 키 조회
def twoSum(self, nums: List[int], target: int) -> List[int]:
nums_map = {}
for i,n in enumerate(nums):
nums_map[n]=i
for i,n in enumerate(nums):
if target-n in nums_map and i != nums_map[target-n]:
return [i,nums_map[target-n]]
중요 내용
- 딕셔너리는 값을 조회하는데 O(1)이 걸리므로 반복문을 실행하는데 O(n)의 시간이 걸린다.
- 실행시간은 앞의 두 풀이 방법보다 훨씬 더 짧게 걸린다.
풀이 4: 조회 구조 개선
def twoSum(self, nums: List[int], target: int) -> List[int]:
nums_map = {}
for i,n in enumerate(nums):
if target-n in nums_map:
return [i,nums_map[target-n]]
nums_map[n]=i
중요 내용
- 풀이3의 반복문 2개를 하나로 묶어서 표현하였다.
풀이 5: 조회 구조 개선
def twoSum(self, nums: List[int], target: int) -> List[int]:
left,right=0, len(nums)-1
while not left==right:
if nums[left] + nums[right] < target:
left += 1
elif nums[left] + nums[right] > target:
right -= 1
else:
return [left,right]
기억해야 할 함수
- list.sort(key= , reverse= ): 리스트를 key에 정한 함수대로 정렬한다. sorted 함수가 정렬된 값을 반환하는 반면 sort 함수는 적용한 리스트를 정렬하고 값을 리턴하지는 않는다.
중요 내용
- 이 방법은 입력 리스트 값이 정렬되어 있음을 가정하였을 때 사용할 수 있는 방법이다. 그러나 이 문제에서는 리스트 값이 정렬되어 있지 않고 정렬하기 위해 sort함수를 사용하면 원래 인덱스가 엉망이 되므로 결과적으로 사용할 수 없는 방법이다.
Question 8: 빗물 트래핑 (재풀이)
높이를 입력받아 비 온 후 얼마나 많은 물이 쌓일 수 있는지 계산
입력: [0,1,0,2,1,0,1,3,2,1,2,1]
출력: 6
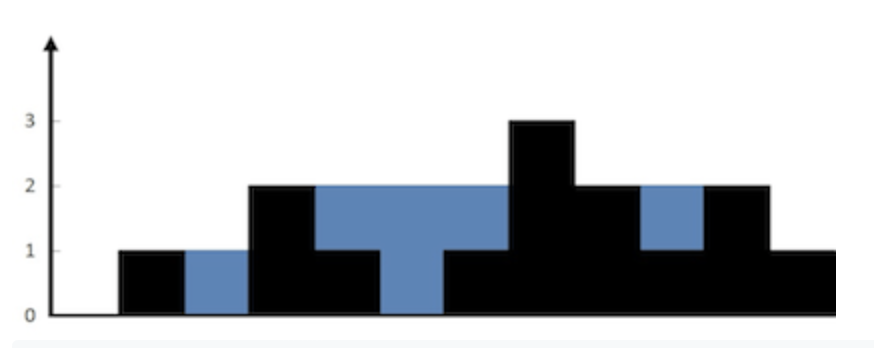
내 풀이: 투 포인터를 최대로 이용
이 문제는 결국 풀지 못하였다. 문제를 보자마자 어떻게 풀어야 할지 감이 안오기도 했고 별 세 개의 난이도 문제이기 때문에 깊게 생각하지 않고 금방 포기한 것도 있었다.
풀이 1: 투 포인터를 최대로 이용
class Solution:
def trap(self, height: List[int]) -> int:
if not height:
return
left_max, right_max = height[0], height[-1]
left, right = 0, len(height)-1
volume = 0
while left < right:
left_max = max(height[left], left_max)
right_max = max(height[right], right_max)
if left_max <= right_max:
volume += left_max - height[left]
left += 1
else:
volume += right_max - height[right]
right -= 1
return volume
기억해야 할 함수
- max(num1, num2, num3, key=function): num1 ~ num3까지 최대 값을 리턴한다. key에서 지정한 함수를 기준으로 가장 최대 값을 리턴한다.
기억해야 할 내용
- 포인터를 이용해 다양한 문제를 푸는 것이 가능할 것이라 생각하지 못했다. 포인터로 문제를 풀 떄의 알고리즘을 psuedocoding 해보았다.
class Solution:
def 함수(self, list: List[int]) -> 원하는 자료형:
left, right = 0, len(height)-1
while left 와 right 비교:
if list[left] 와 list[right] 비교:
left += 1
else:
right -= 1
return 원하는 값
풀이 2: 스택 쌓기
class Solution:
def trap(self, height: List[int]) -> int:
stack = []
volume = 0
for i in range(len(height)):
# 변곡점을 만나는 경우
while stack and height[i] > height[stack[-1]]:
top = stack.pop()
if not len(stack):
break
# 이전과의 차이만큼 물 높이 처리
distance = i - stack[-1] - 1
waters = min(height[i], height[stack[-1]]) - height[top]
volume += distance * waters
stack.append(i)
return volume
기억해야 할 내용
-
이 방법은 현재 높이가 이전 높이보다 더 높을 때, 즉 꺾이는 부분 변곡점을 기준으로 격차만큼 물 높이 volume을 채우는 방법이다. 계속 스택으로 채워 나가다가 변곡점을 만날 때마다 스택에서 하나씩 꺼내면서 이전과의 차이만큼 물 높이를 채워 나간다.
-
for 문으로 한번만 실행하면 풀이가 가능하므로 코드 실행 시간은 O(n) 이다.
-
높이의 차이에 인해서 물이 채워진 부분은 다시 채울 필요가 없으므로 stack 에서 제거된다.
-
변곡점에 도달하면 그 전 기둥의 높이과 min(변곡점의 기둥의 높이, 스택에 있는 기둥의 높이)의 차이를 water로 정의한다.
Question 9: 세 수의 합 (재풀이)
입력: nums = [-1,0,1,2,-1,-4]
출력: [[-1,0,1], [-1,-1,2]]
내 풀이
브루트 포스 방법을 이용하였다
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
three_sum = []
set_three_sum = []
for i in range(len(nums)):
for j in range(i+1,len(nums)):
for k in range(j+1,len(nums)):
if nums[i]+nums[j]+nums[k] == 0 and {nums[i],nums[j],nums[k]} not in set_three_sum:
three_sum.append([nums[i],nums[j],nums[k]])
set_three_sum.append({nums[i],nums[j],nums[k]})
return three_sum
결과
시간 초과 에러가 떴다.
에러 이유
해당 코드에는 반복문이 3개나 들어가 있어 실행 시간이 $O(n^3)$ 걸린다. 이 문제에서는 시간 복잡도를 $O(n^2)$ 이내로 요구하므로 다른 방법을 사용하는 것이 좋다.
풀이 1: 브루트 포스로 계산
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
results = []
nums.sort()
for i in range(len(nums)-2):
if i>0 and nums[i] == nums[i-1]:
continue
for j in range(i+1, len(nums)-1):
if j>i+1 and nums[j] == nums[j-1]:
continue
for k in range(j+1, len(nums)):
if k>j+1 and nums[k] == nums[k-1]:
continue
if nums[i] + nums[j] +nums[k] == 0:
results.append([nums[i], nums[j], nums[k]])
return results
기억해야 할 함수
- 조건문에서 continue는 아래 구문을 실행하지 않고 건너뛴다.
중요 내용
- i>0 and nums[i] == nums[i-1] 는 중복된 값은 계산하지 않고 건너뛰도록 한다.
- 내 풀이와 마찬가지로 시간 복잡도가 $O(n^3)$ 가 걸려 시간 초과 에러가 뜬다.
풀이 2: 투 포인트로 합 계산
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
nums.sort()
result = []
for i in range(len(nums)-2):
if i>0 and nums[i]==nums[i-1]:
continue
left, right = i+1, len(nums)-1
while left<right:
tot = nums[i] + nums[left] + nums[right]
if tot < 0:
left += 1
elif tot > 0:
right -= 1
else:
result.append([nums[i],nums[left],nums[right]])
while left < right and nums[left] == nums[left+1]:
left += 1
while left < right and nums[right] == nums[right-1]:
right -= 1
left += 1
right -= 1
return result
중요 내용
- 이 방법은 직접 손으로 쓰면서 문제를 푸니 직관적으로 이해할 수 있었다. 앞으로 이해가 가지 않는 알고리즘 일수록 손으로 수학문제를 풀듯 쓰면서 이해하자!
- 투 포인터 방법은 리스트가 정렬되어 있을때 사용하는 것이 좋다!
Question 10: 배열 파티션
n개의 페어를 이용한 min(a,b)의 합으로 만들 수 있는 가장 큰 수를 출력하라.
입력: [1,4,3,2]
출력: 4
내 풀이
class Solution:
def arrayPairSum(self, nums: List[int]) -> int:
nums.sort()
result = 0
arr_num = len(nums)-1
for i in range(len(nums)//2):
result = result + min(nums[arr_num-i*2],nums[arr_num-(i*2+1)])
return result
결과
Runtime: 541 ms, faster than 5.26% of Python3 online submissions for Array Partition I.
Memory Usage: 16.8 MB, less than 71.06% of Python3 online submissions for Array Partition I.
- 위와 같은 화면이 뜨며 정상적으로 출력이 된다.
- n이 홀수가 될 수도 있음을 가정하고 코드를 짰지만 이 문제에서는 n이 짝수만 될 수 있다.
- 시간 복잡도는 $O(n)$ 으로 문제가 요구하는 시간보다 길게 나온 것 같다.
풀이 1: 오름차순 풀이
class Solution:
def arrayPairSum(self, nums: List[int]) -> int:
sum = 0
pair = []
nums.sort()
for n in nums:
pair.append(n)
if len(pair) == 2:
sum += min(pair)
pair = []
return sum
중요 내용
- 내 풀이와 시간 복잡도는 동일하게 $O(n)$로 나온다.
- 홀수번째 값은 반복문에 포함될 필요가 없으므로 불필요한 계산이 포함되어 있다.
풀이 2: 짝수 번째 값 계산
class Solution:
def arrayPairSum(self, nums: List[int]) -> int:
nums.sort()
sum = 0
for i,num in enumerate(nums):
if i%2 == 0:
sum += num
return sum
중요 내용
- 정렬된 상태에서는 짝수 번째에 항상 작은 값이 위치해 있으므로 짝수 번 인덱스 값만 더하면 된다.
풀이 3: 파이썬다운 방식
class Solution:
def arrayPairSum(self, nums: List[int]) -> int:
return sum(sorted(nums)[::2])
중요 내용
- list[::2]는 짝수 번째 요소만 슬라이싱 하라는 뜻이다.
Question 11: 자신을 제외한 배열의 곱 (재풀이)
배열을 입력받아 output[i]가 자신을 제외한 나머지 모든 요소의 곱셈 결과 되도록 출력하라.
입력: [1,2,3,4]
출력: [24,12,8,6]
주의: 나눗셈을 하지 않고 O(n)에 풀이하라
내 풀이
class Solution:
def productExceptSelf(self, nums: List[int]) -> List[int]:
left = []
right = []
for i in range(len(nums)):
if i == 0:
left.append(1)
else:
left.append(left[i-1]*nums[i-1])
nums.reverse()
for i in range(len(nums)):
if i == 0:
right.append(1)
else:
right.append(right[i-1]*nums[i-1])
right.reverse()
return (num*num2 for num,num2 in zip(left,right) )
결과
Runtime: 550 ms, faster than 5.03% of Python3 online submissions for Product of Array Except Self.
Memory Usage: 21.8 MB, less than 30.85% of Python3 online submissions for Product of Array Except Self.
- 왼쪽 부분을 곱한 값과 오른쪽 부분을 곱한 값을 서로 곱하였다.
- 시간 복잡도가 $O(n)$ 이지만 다소 불필요한 계산이 많이 들어가 빠르게 실행되지 않았다.
풀이 1: 왼쪽 곱셈 결과에 오른쪽 값 곱셈
class Solution:
def productExceptSelf(self, nums: List[int]) -> List[int]:
out = []
p = 1
for i in range(len(nums)):
out.append(p)
p = p*nums[i]
p = 1
for i in range(len(nums)-1, -1, -1):
out[i] = out[i]*p
p = p*nums[i]
return out
기억해야 할 함수
- for i in range(3, -1, -1) 는 3부터 0까지 -1씩 줄여가며 반복한다.
중요 내용
- 원리는 내가 풀이한 방법과 비슷하지만 계산 과정을 훨씬 더 간단히 하였다.
Question 12: 주식을 사고팔기 가장 좋은 시점
한 번의 거래로 낼 수 있는 최대 이익을 산출하라
입력: [7,1,5,3,6,4]
출력: 5
주의: 나눗셈을 하지 않고 O(n)에 풀이하라
내 풀이
class Solution:
def maxProfit(self, prices: List[int]) -> int:
max_num = 0
for i in range(len(prices)-1):
for j in range(i+1, len(prices)):
max_num=max(prices[j]-prices[i],max_num)
return max_num
결과
시간초과 에러가 떴다.
에러 이유
브루트 포스 방법을 이용하였는데 반복문을 두번 이용해 시간 복잡도가 $O(n^2)$ 가 나왔다. 브루트 포스 방법은 가장 생각해내기 쉬운 풀이 방법이나 계산 과정이 너무 오래 걸리기 때문에 최대한 지양해야 한다고 배웠었다. 브루트 포스 대신 다른 방법을 이용해 문제를 풀려는 습관을 들이자!!
풀이 1: 브루트 포스로 계산
class Solution:
def maxProfit(self, prices: List[int]) -> int:
max_price = 0
for i,price in enumerate(prices):
for j in range(i+1, len(prices)):
max_price=max(prices[j]-prices, max_price)
return max_price
이 방법은 내 풀이 방법과 동일하므로 생략하도록 하겠다.
풀이 2: 저점과 현재 값과의 차이 계산
class Solution:
def maxProfit(self, prices: List[int]) -> int:
profit = 0
min_price = sys.maxsize
for price in prices:
min_price=min(price, min_price)
profit = max(profit, price-min_price)
return profit
기억해야 할 함수
- sys.maxsize는 시스템상에서 표현할 수 있는 가장 큰 값을 표현한다.
중요 내용
- 최솟값과 최댓값을 갱신해야 하는 문제는 min과 max값을 초기에 지정해야 한다. 이 때 최댓값이 되어야 할 변수는 시스템이 표현할 수 있는 가장 작은 값, 최솟값은 시스템이 표현할 수 있는 가장 큰 값을 지정한다. 그래야 어떤 값이 들어오든 바로 갱신할 수 있다.

Comments