Deep Residual Learning for Image Recognition

3 minute read

Introduction

Network depth is of crucial importance for making better models.
However, training and testing error rates increase when number of layer exceeds certain threshold. Graph below proves this.

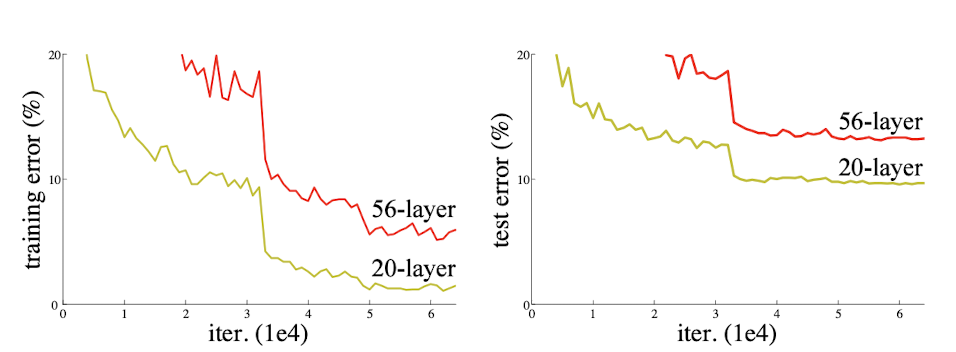
Vanishing and exploding gradient are the cause for such problem.
In this paper, they focused on degradation, suggesting deep residual learning framework to address this problem.

The goal of this techinque is to construct layers with identity mapping, which is to make the input and output identical.
Rather than directly fitting input data to output data, resiudal learning focuses on fitting input data to residual function, which is the residue of output and input data.

Let us consider the equation below, which $H(x)$ stands for output data, $x$ for input data and $F(x)$ for residual function.

$H(x) = F(x) + x$
To make identity mapping possible, $F(x)$ should become 0.
$F(x)$ is expressed as $F(x) = H(x) -x$
Now, the training process involves making $F(x)$ 0.
Dimensions of both input and ouput data should be identical to train residual function.

$y = F(x, {W_i}) + x$

function $F(x, {W_i})$ represents residual mapping to be learned
With 2-layer model, residual block is defined as: $F = W_2\sigma(W_1x)$
The equation above is interpreted as having shortcut connection to output $y$.
Shortcut connection resolves the previous issues of identity mapping by introducing neither extra parameters nor computational complexity.
When dimensions of $F$ and $x$ are different, adding linear projection $W_s$ is performed to make these two dimensions identical.
Above notations are about fully connected layers, but this is applicable to convolutional layers as well.

This section introduces models that are used for evaluating the performace of residual network.
VGGNet with 34 weighted layers is used as plain network and VGGNet with shortcut connection inserted is used as resiudal network.
Following 2 options were used to prevent the problem of dimension increase.
1. Extra zero entries are padded for increasing dimension.
2. Projection techinque, which is adding $W_s$ to residual function, is used to match dimension.

Two networks are evaluated on the ImageNet 2012 classification dataset that consists of 1000 classes.
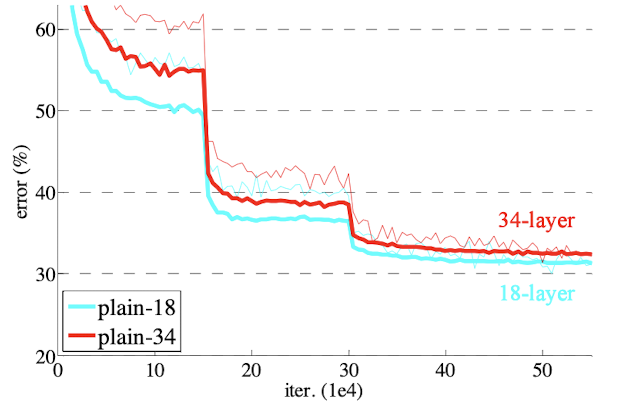
Plain network with 34 layer shows higher training error rate than that with 18 layer. This paper conjectures that this is not due to vanishing gradient, but it is due to having exponentially low convergence rates.

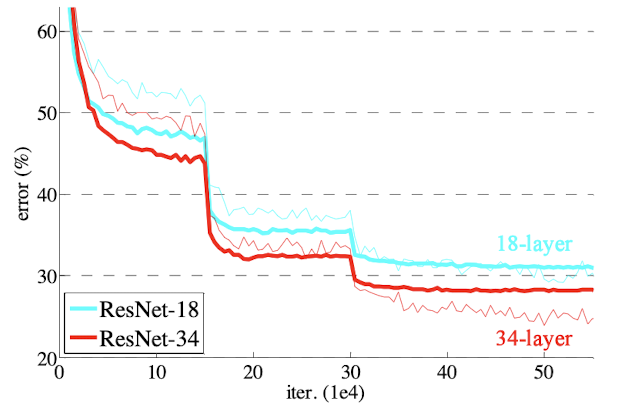
However, the situation is reveresed for residual networks. Residual networks with 34 layer shows lower training error rate than that with 18 layer.

Additionally, the classification tasks are given in these 3 different tasks:
1. Zero padding shortcuts are used for increasing dimensions.
2. Projection shortcuts are used for increasing dimensions.
3. All shortcuts are projections.

Table below shows that all these three models are considerable better model than plain counterpart.

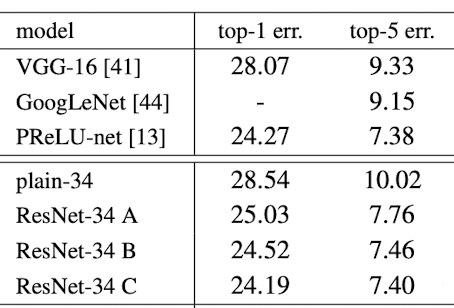
Small difference in errors for these 3 options exhibits that projection shortcuts are not essential for building better performing model.

CIFAR-10 dataset consists of 50k training images and 10k test images in 10 classes.
Model used for classification follow the same form with that used in ImageNet classification, which has a total of 6n+2 weighted layers. Feature map sizes are 32, 16, 8, respectively.
Input images are 32x32 with per-pixel mean subtracted (This is probably done for scaling).
The last two layers consists of global average pooling and a 10-way fully-connected layer with softmax.
Graph below compares the error rate of plain networks and ResNet. Dashed line denotes training error and bold line denotes testing error.

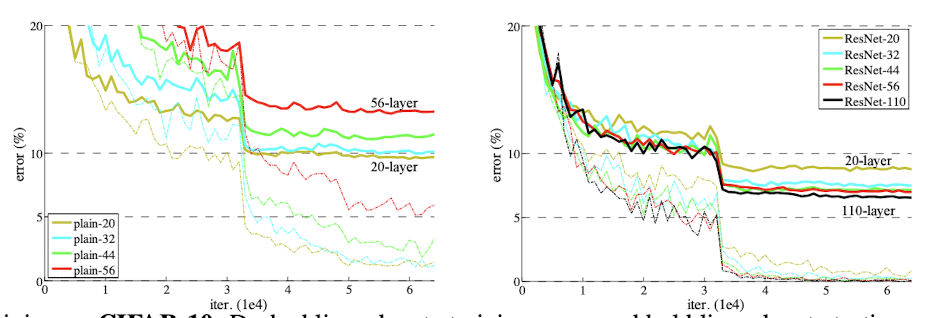
Error rate of deeper plain network is higher than that of shallower network for both training and test data.
Unlike plain network, error rate of deeper ResNet is lower than that of shallower network.
However, ResNet also suffers from overfitting problem when number of layer reaches 1202. Therefore, it is better to use adequate number of layers to prevent models from getting too complex.