Understanding Diffusion Models Towards Adversarial Robustness

1. Introduction

• Diffusion model (이하 DM)은 likelihood-based 모델로, 생성하는 샘플 퀄리티가 좋은 동시에 GAN이 가지고 있던 mode collapse issue를 효과적으로 해결하고 있다.

• DM은 input image에 노이즈를 주기적으로 추가하는 forward process와 노이즈를 제거해 나가는 reverse process로 구성되어 있다.

• Empirical research를 통해 DM이 adversarial attack을 효과적으로 제거한다는 것이 나타났지만 이에 대한 구체적인 이유에 대해서는 아직 연구되지 않았다.

• 이 논문에서는 DM이 adversarial attack을 1. 어떻게 효과적으로 제거하는지와 이를 통해 2. DM을 통해 모델을 robust하게 만드는 새로운 framework인 DensePure을 제시한다.

2. Preliminaries and Backgrounds

1. Continuous-Time Diffusion Model

‘Score-based generative modeling through stochastic differential equations.’ 논문에서는 Score-based generative model들은 SDE(Stochastic Differential Equation) framework안에서 크게 두가지 요소인 diffusion forward process와 reverse process로 구성되어 있다고 주장하고 있다. 먼저 forward diffusion process은 다음과 같이 나타낼 수 있다.

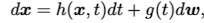
다음으로 reverse process는 다음과 같이 reverse-time SDE로 나타낼 수 있다.

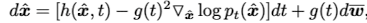
2. Discrete-Time Diffusion Model(or DDPM)

‘Denoising Diffusion Probablistic Model’논문에서는 DDPM의 forward diffusion process를 다음과 같이 나타낸다.

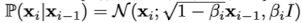
Reverse diffusion process는 다음과 같이 나타낸다.

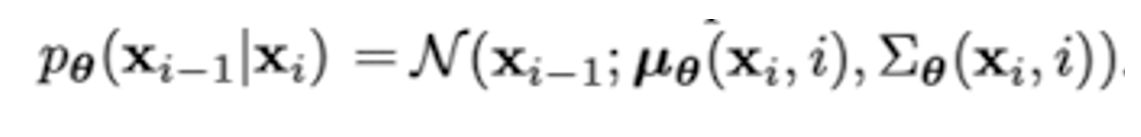
여기서 이 논문에서는 다음 step에서 노이즈를 제거한 샘플 분포의 분산을 $\beta_i$ ($i$번째 step에 주입한 노이즈의 양) 으로 고정하고, 평균인 $\mu_\theta (x_i, i)$ 만을 구하는 것으로 간단히 하였다. 손실 함수를 계산하는 과정이 워낙 복잡하기 때문에 이 과정을 생략하고 최종적인 손실 함수만을 나타내면 다음과 같이 나타낼 수 있다.

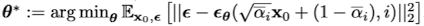
위 공식은 곧 $i$번째 step에서 노이즈를 추가한 이미지를 입력 값으로 넣었을 때 추가한 노이즈의 양을 출력하는 네트워크를 구성하는 것을 목표로 한다는 것으로 이해할 수 있다.

3. Randomized Smoothing

RS(Randomized Smoothing)은 $L_2$-norm에 해당되는 adversarial attack을 효과적으로 막기 위해 고안된 방법이다. 다음과 같은 방법으로 classifier을 smoothing 해줌으로써 classifier을 robust하게 만들어준다.

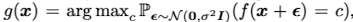
여기서 $\sigma$는 모델의 robustness와 accuracy를 조절하는 parameter이다. 아직 해당 논문을 읽어보지 않았기 때문에 자세한 이해를 위해 추가로 읽어 볼 예정이다.

3. Theoretical Analysis

해당 섹션에서는 DM이 어떻게 adversarial attack을 효과적으로 제거하는지에 대해 다음과 같은 3가지 Theorem을 통해 밝혀내고 있다. 먼저 해당 섹션의 Theorem들은 다음과 같은 가정을 만족하고 있다.

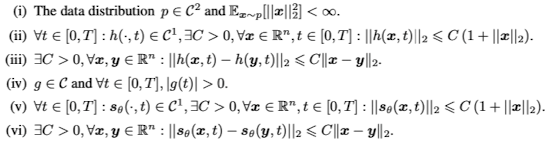
Theorem 3.1

Perturbed된 데이터 포인트인 $x_{a,t}$가 reverse-SDE를 거치고 난 후 purify된 데이터 포인트 $\hat{x}$ 는 다음과 같은 조건부 확률분포를 가진다.

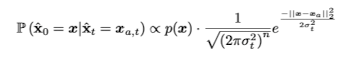
위 공식을 통해 $\mathbb{P}$를 증가시키기 위해서는 $\left | x-x_a \right |_2^2$를 감소시켜야 하고, 이는 곧 $x$가 $x_a$ 주변으로 높은 밀도를 가져야 함을 알 수 있다. 따라서 다음과 같이 $\mathbb{P}$를 최대화하는 데이터 포인트 $x$를 선택하는 것으로 간단히 나타낼 수 있다.

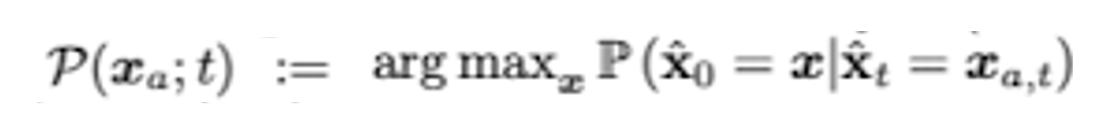
Theorem 3.2

$f$가 classifier이고 $G(x_0)$가 $x_0$과 같은 class를 가지는 data region이라고 하자. 여기서 $P(\cdot ;\psi)$가 purification model 이라고 할 때 $G(x_0)$의 robust data region은 다음과 같이 정의할 수 있다.

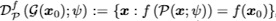
위 식은 purified 된 $x$가 $x_0$과 같은 label을 가지는 $x$의 집합을 나타내는 robust data region이라고 해석할 수 있다.
또한 $x_0$의 robust radius는 다음과 같이 정의할 수 있다.

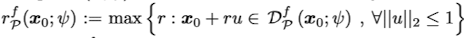
위 식은 곧 $x_0$을 둘러싸고 있는 $D(x_0 ; \psi)$ 의 maximum inclined ball의 반지름이다.

결국 Theorem 3.2를 통해 나타내고 싶은 것은 다음과 같다:
$x_a$가 Euculidean distance 상으로 $x_0$과 충분히 가까울 때 $x_a$는 $x_0$와 purified 된 sample인 $P(x_a;t)$과 같은 label semantics를 유지하고 같은 label로 분류 한다. 그러나 $x_a$가 $x_0$와 가깝지 않아도 $x_0$과 같은 label을 가지고 있는 다른 데이터 포인트, $ \tilde{x}$와 가까워도 $x_0$와 같은 label로 분류한다. 이것에 대한 증명을 다음 Theorem에서 한다.

Theorem 3.3

1. $x_0$가 ground truth label을 가지고 있는 data point이고 $x_a$가 perturbed 된 $x_0$라면 purified된 $P(x_a;t)$는 다음과 같은 convex set에 포함될 때 $x_0$와 같은 label을 가진다.

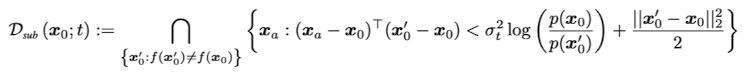
2. 또한 $x_a$는 다음과 같은 convex set에 포함될 때 $x_0$과 같은 label을 가진다.

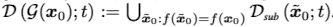
여기서 1과 2의 다른 점은 2는 $x_0$과 같은 레이블을 가진 다른 데이터 포인트 $\tilde{x}$를 사용한다는 점이다.

결국 robust radius인 $r(G(x_0);t$를 찾는 것이 이 문제의 핵심이라고 할 수 있다. 여기서 한가지 주의해야 할 점이 있다. 바로 $D_{sub}(x_0 ; t)$는 convex여도 $D(G(x_0);t)$는 convex가 아니라는 점이다. 따라서 $D(G(x_0);t)$를 해결하기 위해서는 다음과 같은 방법으로 문제에 접근해야 한다.

1. non-convex optimization 방법을 이용해야 한다.
2. $D_{sub}(x_0 ; t)$는 convex이므로 convex optimization을 이용해 해결해서 $r(G(x_0);t$에 대한 lower bound를 찾을 수 있다.

이 논문에서는 2번의 방법으로 접근하고 있다. (그 이유에 대해서 간단하게 설명하고 있으나 convex optimization에 대해서 따로 공부를 하지 않아 이해를 하지 못했다. 추후에 공부한 후 이 부분에 대해서는 다시 작성하도록 하겠다.) 그러나 $D(G(x_0);t)$는 다른 sub region들을 합집합 한 것이므로 sub region보다 훨씬 더 커질 위험이 있다. 이것에 대해서 해당 논문에서는 아래와 같은 figure을 통해 설명하고 있다.

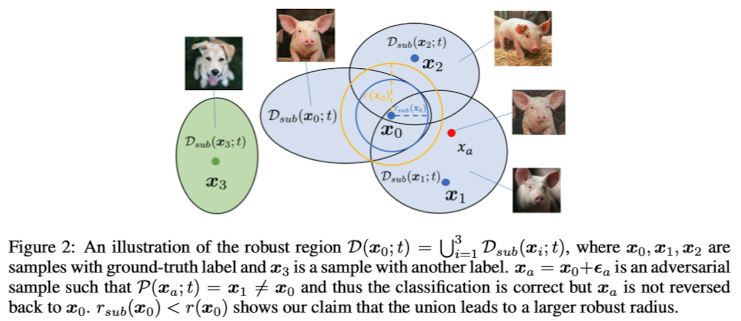
따라서 reverse-SDE를 통해 정확한 값을 찾는 것 대신에 approximation 방법을 이용하고 있다. approximation 방법에는 예시로 score-based model을 사용해 reverse-SDE와의 KL-Divergence를 나타낸 것이 Theorem 3.4이다.
여기서 convex에 대해 아는 것이 거의 없었기 때문에 convexity를 보존하는 연산에 대해서 별도로 찾아보았다. convex set의 convexity를 보존하는 연산은 다음과 같다.

1. Intersection
2. Scaling and transition
   예시) $C$가 convex set이고 $a$, $b$가 각각 scaling, transition scalar factor이면 $aC+b$ 또한 convex set이다.
3. Affine images and preimages
   예시) $f(x)=Ax+b$이고 C가 convex set이면 $f(C)$도 convex set이다. 또한 D가 convex set이면 $f^{-1}(D)$ 또한 convex set이다.

Theorem 3.4

$\lVert {\hat{x_\gamma} \rVert }_{\gamma \in [0, t]}$ 와$\lVert {x^{\theta}_\gamma \rVert }_{\gamma \in [0, t]}$가 각각 reverse-SDE, score-based diffusion model이라고 하면 이 두 분포의 KL-Divergence는 다음과 같이 나타낼 수 있다.

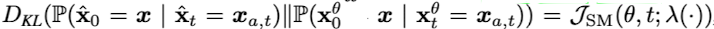
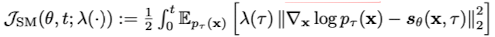
DensePure

지금까지 증명한 내용을 바탕으로 DM을 통해 모델을 robust하게 만드는 새로운 framework인 DensePure 을 새로 제안하고 있다. 이 framework가 작동하는 순서는 다음과 같다.

1. 입력값 $x$가 reverse process를 거쳐서 $rev(x)$를 얻는다.
2. 1번 과정을 K번 반복하여 ${rev(x)_1,…,rev(x)_K}$를 얻는다.
3. ${rev(x)_1,…,rev(x)_K}$를 classifier에 통과시켜 그 중에서 가장 많이 나온 label을 최종 예측값으로 설정한다. 이렇게 가장 많이 나오는 label을 찾는 과정을 Majority Vote, 줄여서 MV라고 한다.

또한 DensePure에

1. Randomized Smoothing을 적용해 $L_2$-norm adversarial attack을 효과적으로 막는 것에 대한 증명과
2. Improved Denoising Diffusion Probablistic Models에 사용된 Fast Sampling 기법을 사용해 더 빠르게 샘플링하는 과정에 대해서 설명하고 있으나 중요한 내용은 아니므로 생략하도록 하겠다.
   다음은 DensePure의 pipeline에 대해 나타낸 figure이다.

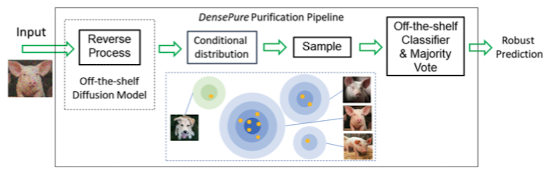
Experiments

아래는 다른 baseline method와의 성능 비교를 통해 나타난 결과이다. 데이터셋은 CIFAR-10, ImageNet을 사용하였다.

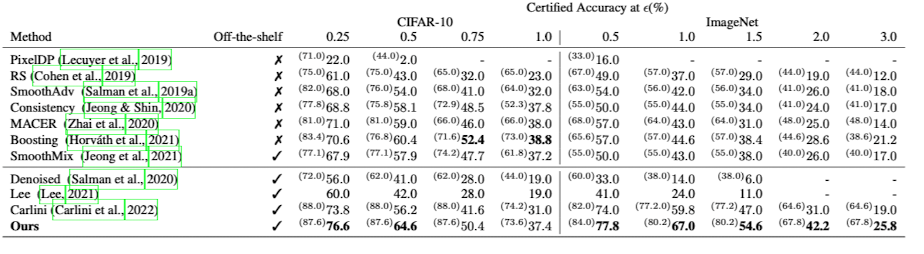
여기서 $\epsilon$은 adversarial attack에 의해 perturbed된 비율이고, 각 정확도 수치 옆에 괄호는 $\epsilon=0$ 일 때의 정확도이다. 즉, standard accuracy 이다. 또한 off-the-shelf는 모델이나 classifier의 별도의 학습을 요구하지 않는 plug-and-play manner로 작동하는 method를 지칭한다. 결과표를 보면 알 수 있듯이 다른 방법들과 비교를 했을 때 거의 모든 $\epsilon$에 대해서 SOTA를 달성하고 있다는 것을 알 수 있다.

또한 DensePure과 비슷하게 DM을 사용한 논문인’(certified!!) adversarial robustness for free!’ 와의 성능 비교를 하고있다. 다음 그래프는 CIFAR-10, ImageNet 데이터셋에 대한 비교 결과이다.

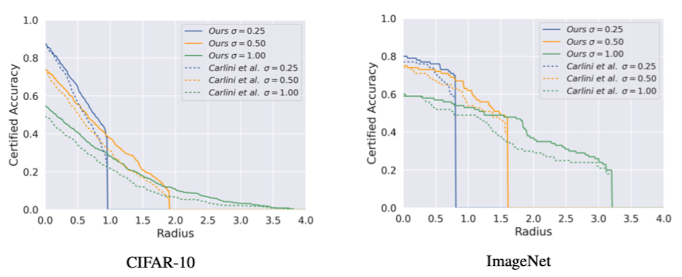
모든 noise scale $\sigma$에 대해서 DensePure가 더 좋은 성능을 보이는 것을 알 수 있다.

Ablation study

아래 figure은 Voting sample의 $K$값과 Fast sampling steps $b$에 대한 ablation study를 진행한 결과이다.

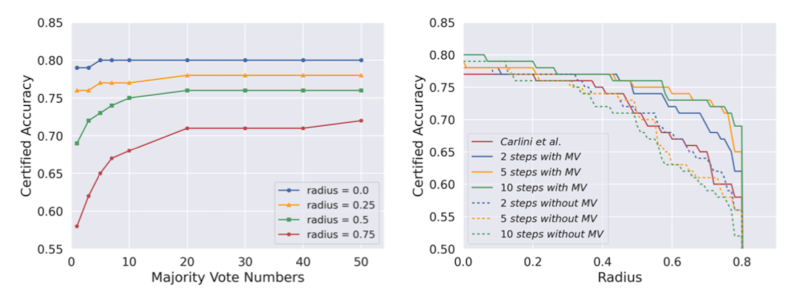
결과표를 통해 다음과 같은 사실을 알 수 있다.

1. $K$값이 증가할 때마다 정확도가 증가한다.
2. MV(Majority Vote)가 사용되면 sampling step이 증가할 때마다 정확도가 증가하지만, MV(Majority Vote)가 사용되지 않으면 sampling step이 증가할 때마다 정확도가 감소한다.

Limitations

MV에 사용되는 reverse process 때문에 time complexity가 매우 높게 나타난다. 해당 논문에서는 이러한 문제를 극복하기 위해 fast sampling 방법을 사용했지만 문제가 완전히 해결된 것은 아니기 때문에 더 발전된 fast sampling 방법이 필요할 것이다.