Lecture 14: Reinforcement Learning
이번 단원에서는 강화 학습(reinforcement learning)에 대해서 다루고 있다.
What is reinforcement learning?
강화학습(reinforcement learning)은 어떤 환경 안에서 정의된 에이전트가 현재의 상태를 인식하여, 선택 가능한 행동들 중 보상을 최대화하는 행동 혹은 행동 순서를 선택하는 방법이다. 강화학습이 일어나는 과정은 다음과 같다.
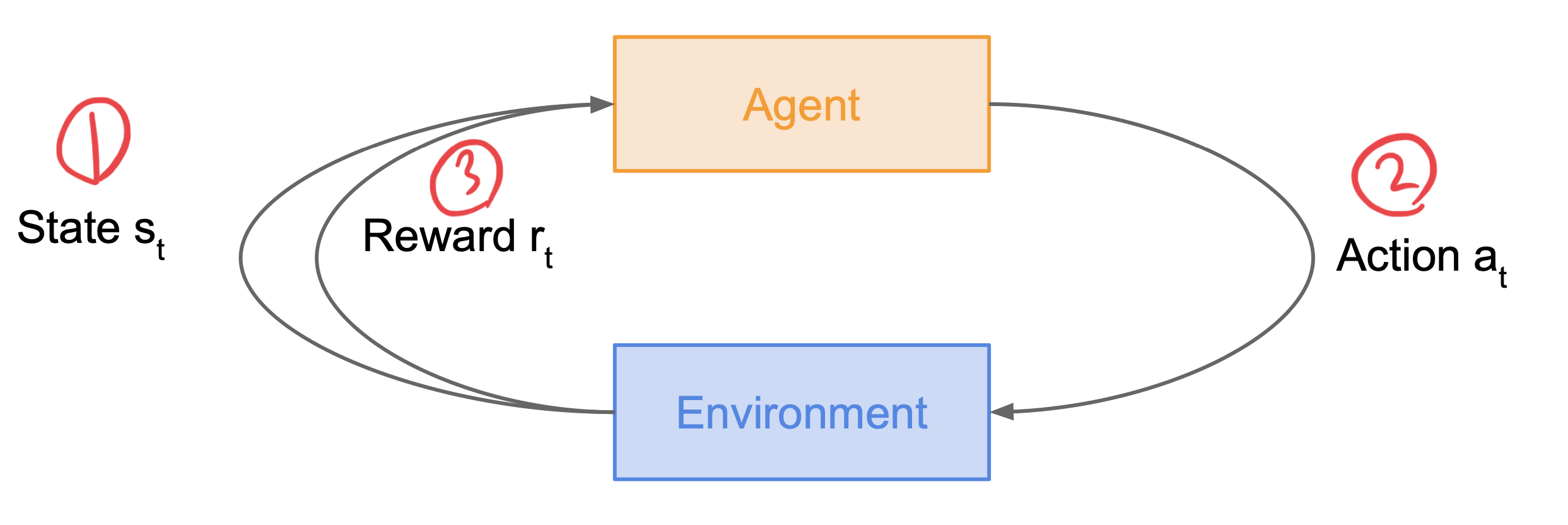
- 에이전트가 $s_t$ 상태에 놓인다.
- 에이전트가 $a_t$ 행동을 취한다.
- 에이전트가 취한 행동에 따른 보상을 받는다.
위 과정과 같이 행동과 그에 따른 보상을 받는 것을 반복하며 강화학습이 일어나게 된다.
Formulation of reinforcement learning
강화학습은 Markov property을 활용하여 나타낼 수 있다. Markov property란 이 세계의 모든 상태들을 수식으로 나타낸 것이다. 이 수식의 형태는 다음과 같다.

Markov property를 이용하여 에이전트가 취할 행동을 확률적으로 나타낸 것이 Markov Decision Process이다. 이 과정은 다음과 같은 순서로 일어난다.

여기서 policy (한글로 직역시 정책이나 표현이 어색하여 영단어 그대로 사용할 것이다) $\pi$란 S에서 어떠한 A를 선택할지 결정하는 함수이다. 따라서 최대 보상을 받기 위한 $\pi^{*}$를 찾는 것이 강화학습의 목적이다.
Value function and Q-value function
Value function
Value function이란 s상태에 놓인 에이전트가 policy를 따랐을때 받는 누적 보상을 나타내는 함수이다. 상태가 얼마나 좋은지 평가하기 위해 사용되는 함수이다. 이 함수의 형태는 다음과 같다.
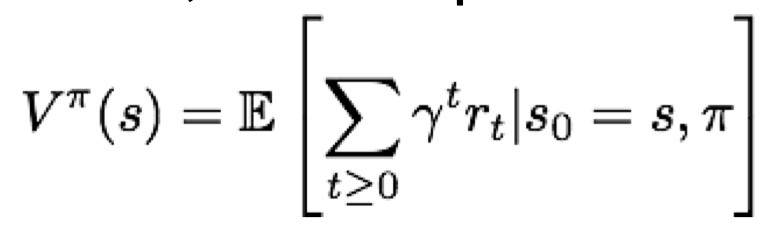
Q-value function
Q-value function이란 s상태에 놓인 에이전트가 a행동을 취한 후 policy를 따랐을때 받는 누적 보상을 나타내는 함수이다. s와 a로 함수가 나타나기 때문에 상태-행동 짝이 얼마나 좋은지 평가하기 위한 지표로 사용된다. 이 함수의 형태는 다음과 같다.
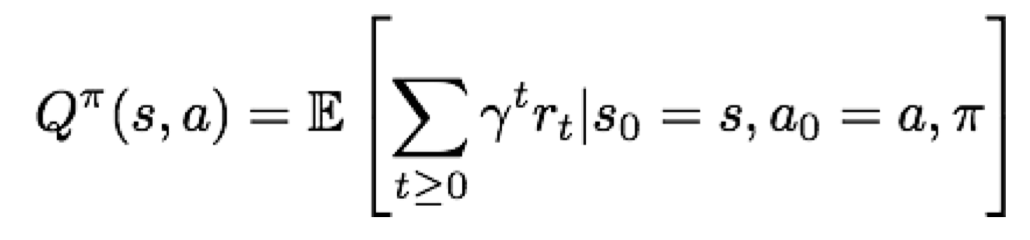
Bellman equation
Bellman equation은 Q-value function에서 가장 높은 누적 보상 값을 만족하는 상태-행동 짝으로 나타낸 함수이다. 즉, $Q^{*}$은 다음과 같은 수식을 만족한다.
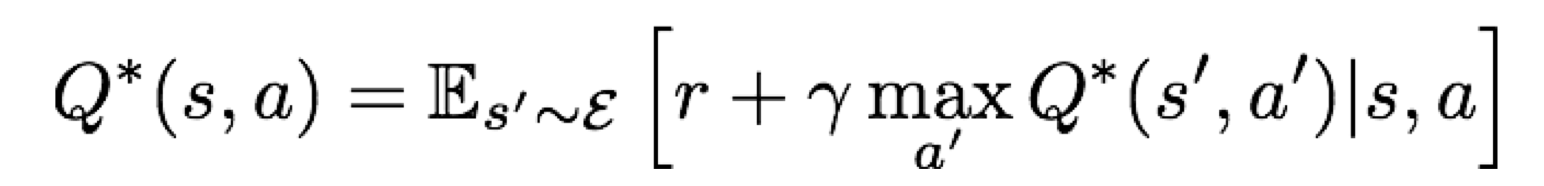
이때 $Q_{i}(s,a)$ 의 다음 값인 $Q_{i+1}(s,a)$를 알고 있는 경우 이 값을 Bellman equation에 대입하여 무한대로 보내면 $Q_{i}$는 $Q^{*}$로 수렴하여 값을 얻을 수 있게 된다. 그러나 이렇게 계산을 하게되면 모든 상태-행동 짝에 대해 Q값을 구해야하므로 계산량이 엄청나게 많아지게 된다. 따라서 이를 해결하기 위한 방법으로 고안된 것이 Q-learning 이다.
Q-learning
Q-learning은 Bellman equation을 인공신경망으로 치환하여 치환한 인공신경망으로 대신 계산하는 방법이다. 여기서 순전파와 역전파를 할때 손실함수, gradient update 의 모습을 다음과 같은 수식으로 나타낼 수 있다.
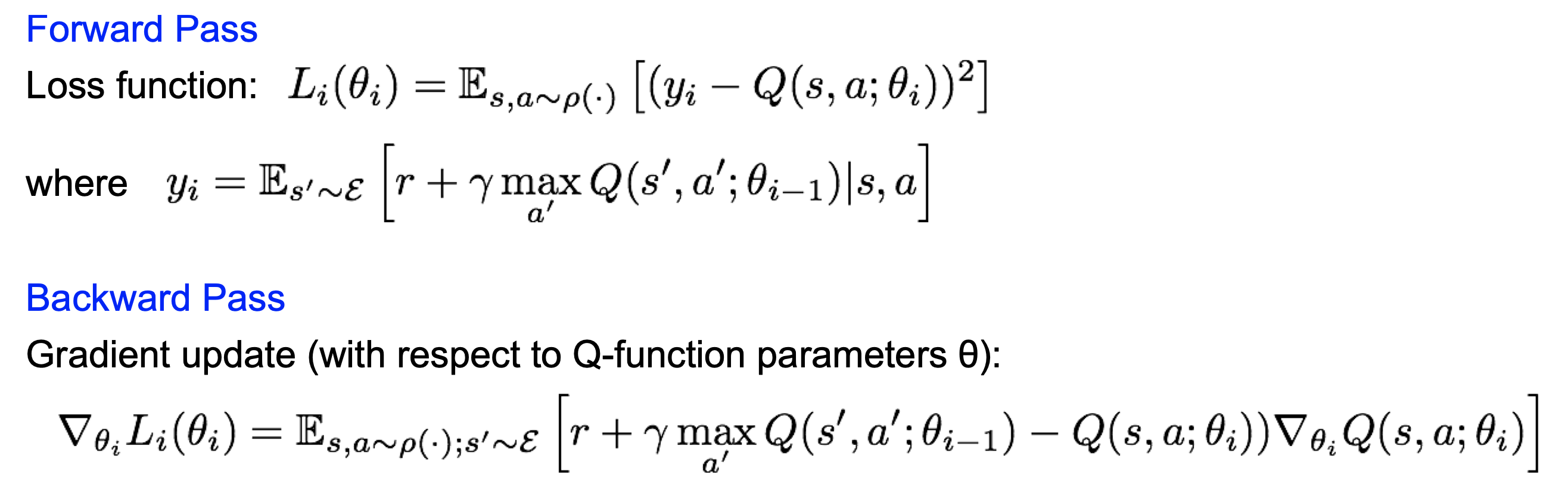
위의 함수에서 $y_i$는 타겟 값, 즉 $Q_{i}$를 나타낸다. 따라서 최적의 $Q_{i}$를 찾기 위한 s,a와 가중치 값을 정하는 것이 이 인공신경망의 목적이라고 할 수 있다.
Playing Atari game
아타리 게임에 강화학습을 적용해보았다. 여기서,
- 목표는 가장 높은 점수를 내는 것,
- 상태는 게임 화면의 픽셀,
- 행동은 앞,뒤,좌,우와 같은 게임 컨트롤,
- 보상은 점수의 증가/감소 이다.
행동이 4번 있다고 했을 때 다음과 같이 입력 값과 출력 값이 나타나게 된다.
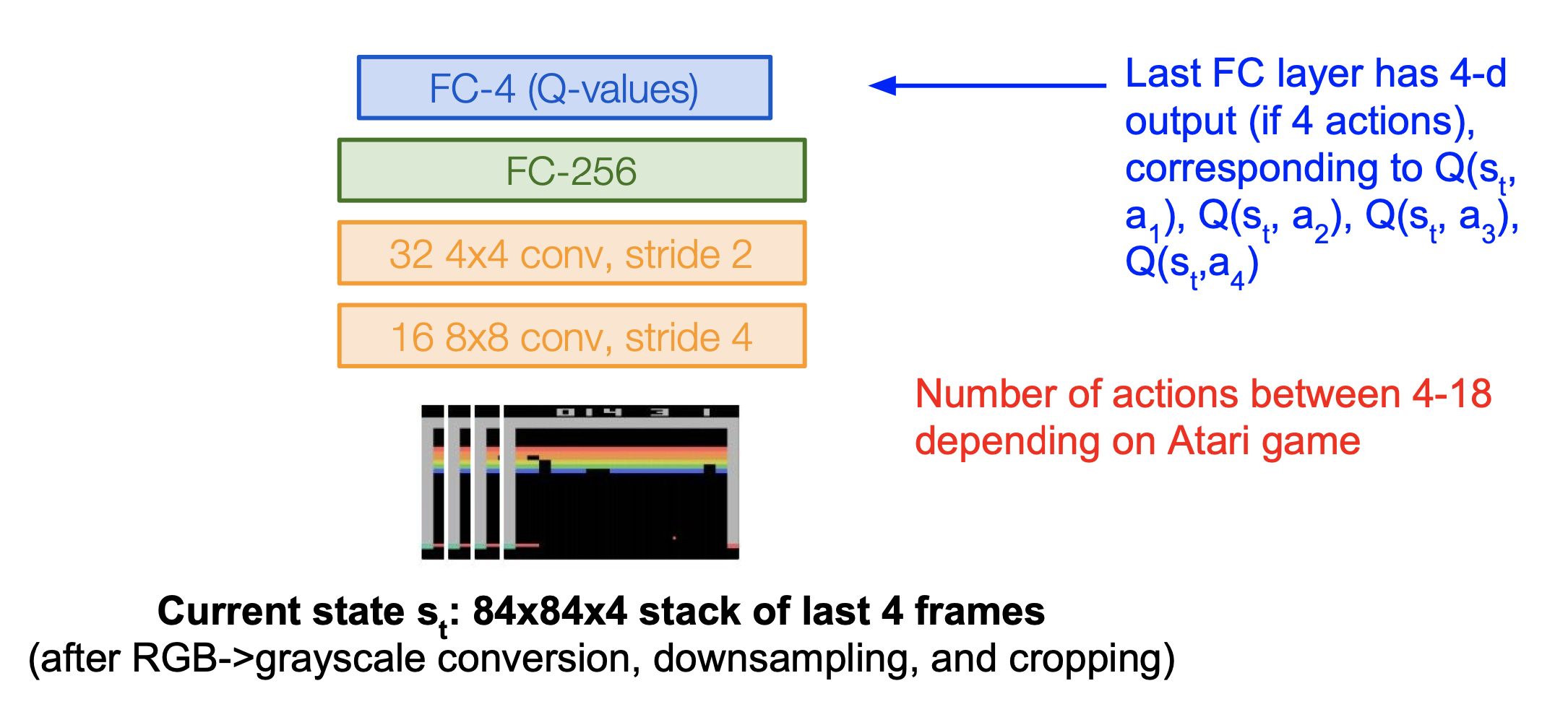
즉, 4번의 행동에 대한 4개의 상태-행동 짝이 나타나게 된다. 여기서 순전파 과정이 한번만 일어나 Q-value를 구할 수 있기 때문에 계산이 매우 간단해진다.
Policy Gradients
Q-learning은 사실 모든 행동에 대한 상태-행동 짝을 구해야하므로 필요없는 계산이 매우 많아질 수 있다. 만약 로봇이 물체를 집는 모습을 가정하자. 이때 이러한 행동을 하기까지 모든 중간과정의 상태-행동 값을 구해야 한다. 하지만 특정 상태에서 특정 행동을 바로 행할 수 있는 policy를 배우면 이러한 중간 과정은 생략되고 로봇은 바로 물체를 집을 수 있게 된다. 이러한 최적의 policy를 구하기 위한 방법이 바로 policy Gradient 이다. Policy Gradient의 원리는 다음과 같다.
인수로 나타낼 수 있는(parametrized) 여러개의 policy가 속한 집합이 있다고 하자. 그 집합의 모습은 다음과 같다.
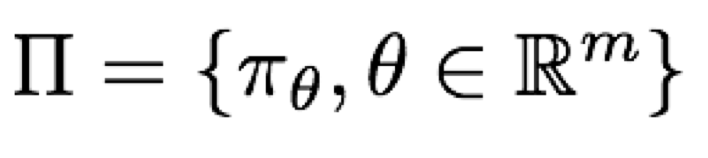
그리고 각 policy의 값은 다음과 같이 나타낼 수 있다.
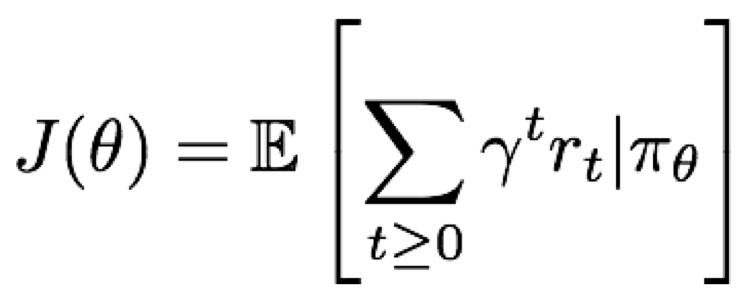
여기서 우리가 찾고 싶은 것은 최적의 policy 값, 즉 가장 큰 policy 값이다.
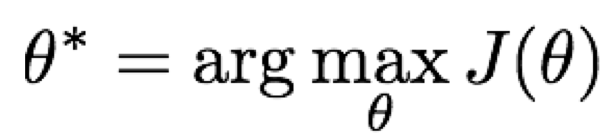
최적의 policy 값을 찾기 위해서는 policy 인수에 gradient ascent를 적용하면 된다. gradient ascent를 하는 과정은 상당히 복잡해져 이 과정은 생략하도록 하겠다. 이 과정을 REINFORCE 알고리즘이라고 하는데, 간단하게 이 알고리즘에 대한 결과만 설명하도록 하겠다.
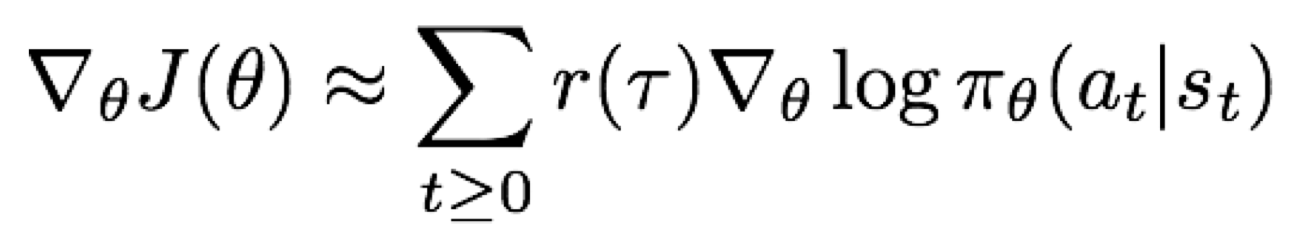
여기서 $r(\tau)$는 각 policy에 대한 보상값이다. 위 식은 다음과 같이 해석할 수 있다.
- 만약 $r(\tau)$가 높으면 행동을 증가시킨다.
- 만약 $r(\tau)$가 낮으면 행동을 감소시킨다.
따라서 $r(\tau)$가 따르는 경로가 좋은 경우(중간 행동들에 대한 보상들이 높은 경우) 그 경로에 해당하는 모든 행동이 좋다고 해석할 수 있다. 그러나 사실 그것은 최적의 policy가 나타나기 위한 모든 행동들이 평균되어 나타난 값이므로 어떠한 행동이 가장 좋은 행동인지에 대해서는 알지 못하게 된다. 따라서 이를 알기 위해서 variance reduction, 즉 표본의 분산을 줄이는 작업을 해야한다. 이 과정에 대해서는 다소 복잡하고 도움이 되는 내용이 아니라 판단되어 생략하도록 하겠다.
REINFORCE in action: Recurrent Attention Model (RAM)
RAM이란 이미지를 분류할때 이미지의 모든 픽셀이 아닌 특정 픽셀만 보고 바로 분류를 할 수 있게 만드는 모델이다. 이 모델의 분류 과정은 다음과 같이 이루어진다. 먼저 강화학습의 목적, 상태, 행동, 보상을 정의하자.
- 목표는 이미지 분류,
- 상태는 이미지의 일정 부분,
- 행동은 어떠한 이미지의 일정 부분의 중심(x,y 좌표)을 볼 것인가,
- 보상은 제대로 분류를 하면 1, 분류를 하지 못하면 0을 부여한다 이다.
다음은 모델을 통해 이미지에서 분류를 위한 중요한 부분을 찾아나가는 과정이다.
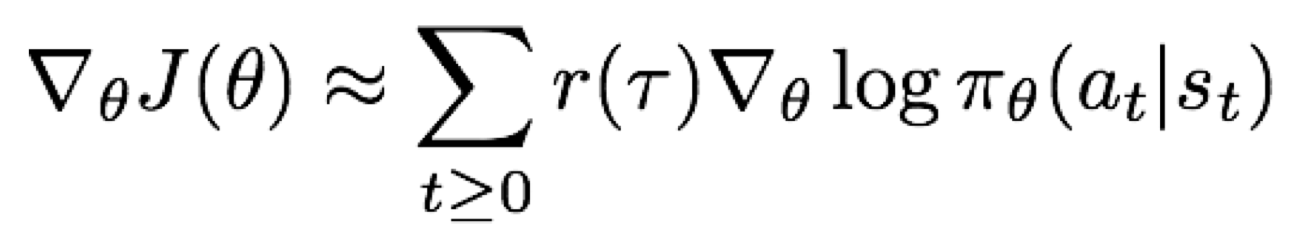
이렇게 차례로 좌표값을 바꾸며 보상에 따른 상태를 바꾸게 되는 과정을 반복하다보면 이미지를 알맞게 분류할 수 있게 된다.
이 강의는 알파고의 원리에 대해서도 가볍게 다루고 있다. 알파고도 강화학습의 결과라는 것 정도만 기억하고 있으면 될 것이다.
Summary
-
Policy gradient: Q-learning의 계산의 복잡성 문제를 보완하기 위해 만들어진 방법이다. 가장 보편적으로 사용되는 방법이나 표본의 분산문제 때문에 variance reduction을 실행해야 한다.
-
Q-learning: 모든 행동-상태 짝에 대한 Q값을 구해야 하기 때문에 policy gradient 보다 다소 복잡한 계산을 요구한다. Policy gradient보단 보편적이진 않지만 한번 작동에 성공하면 더 좋은 성능을 낸다.

Comments