Lecture 3: Loss Function and Optimization

What is Loss Function?

손실함수(loss function) 은 분류기 (classifier)가 얼마나 잘 작동하는지 알려주는 중요한 지표이다. 손실함수의 공식은 다음과 같다.

$L=\frac{1}{N}\sum_i L_i(f(x_i,w),y_i)$

여기서 $x_i$는 이미지, $y_i$는 레이블이다.

Multiclass SVM(Support Vector Machine) loss

Multiclass SVM loss 는 예측한 레이블의 점수 와 카테고리별 점수 의 차를 계산하여 만약 0보다 작으면 0이, 0보다 크면 그 차이값이 채택이 된다. 그리고 채택이 된 값을 모두 더한다. 식으로 표현하면 다음과 같다.

$L_i=\sum_{j\neq y_i} max(0,s_j-s_{y_i}+1)$

여기서 $s_j$는 예측한 레이블의 점수, $s_{y_i}$는 클래스별 점수 이다. 뒤에 붙는 숫자 1은 단지 임의로 설정한 값으로, $s_j-s_{y_i}$ 값이 0이 될 때 0과 비교했을 때 더 큰 값이 나오도록 하는 역할을 한다.

예시로 다음과 같은 3개의 다른 카테고리의 사진과 클래스별 점수가 있다.

여기서 고양이 사진의 손실, 즉 $L_1$ 의 값은 $max(0,5.1-3.2+1)+max(0,-1.7-3.2+1) = 2.9+0 = 2.9$ 이다. 차 사진의 손실과 개구리 사진의 손실도 같은 방법으로 다음과 같이 구할 수 있다.

$L_2=max(0,1.3-4.9+1)+max(0,2-4.9+1) = 0$ $L_3=max(0,2.2-(-3.1)+1)+max(0,2.5-(-3.1)+1) = 6.3+6.6 = 12.9$

$L_1, L_2, L_3$ 의 평균은 $\frac{2.9+0+12.9}{3} = 5.27$ 이고 이 점수가 이 분류기의 손실값 이다.
Multiclass SVM loss의 몇 가지 특징을 살펴보면 다음과 같다.

Features of Multiclass SVM loss

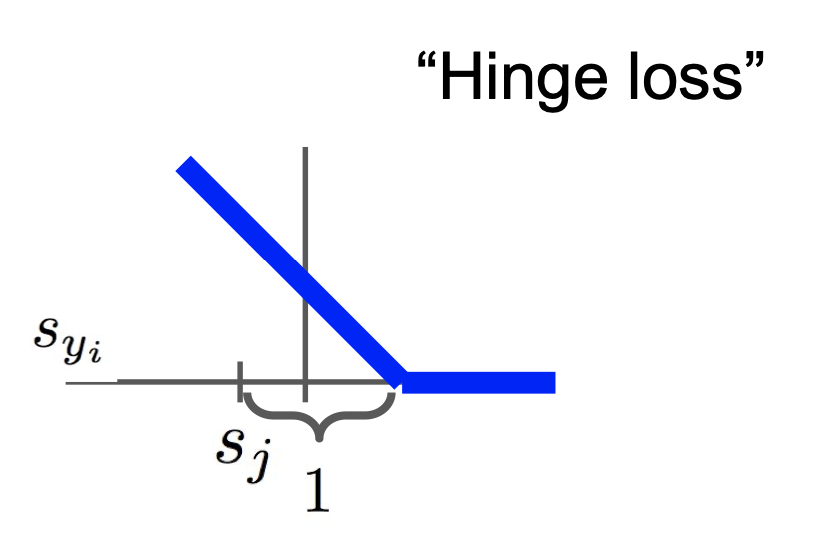
1. 예측한 레이블의 점수는 그대로이고 실제 레이블의 점수가 증가하면 손실 값의 크기가 감소한다. 아래 그래프는 이를 나타내었다.

1. 손실값은 최소 0 (완벽하게 분류함), 최대 무한대 (하나도 분류를 못함)의 값을 가질 수 있다.

2. 손실값을 0으로 만드는 가중치 $W$ 이 있다고 할 때 $2W$ 또한 손실값을 0으로 만든다.

3. Multiclass SVM loss 를 파이썬 코드로 구현하면 다음과 같다.

def L_i_vectorized(x,y,W):
    scores = W.dot(x)
    margins = np.maximum(0, scores-scores[y]+1)
    margins[y] = 0
    loss_i = np.sum(margins)
    return loss_i

앞서 설명한 함수를 그대로 표현한 것이므로 코드에 대한 별도의 설명은 생략하도록 하겠다.

Regularization

Regularization, 즉 정칙화는 모델이 훈련 데이터에 과적합하는 것을 방지 하고 단순하게 만들기 위해 사용된다. 정칙화 함수는 손실함수 뒤에 붙게된다. Normalization이 정규화, Regularization이 정칙화 이므로 이 두개의 단어를 잘 구분하여 사용하도록 하자.

$L=\frac{1}{N}\sum_i L_i(f(x_i,w),y_i)+\Lambda R(w)$

정칙화에는 대표적으로 L2 정칙화, L1 정칙화 가 있다. 각각의 공식은 다음과 같다.

• L2 정칙화: $R(W)=\sum_k\sum _l{W^2}$
• L1 정칙화: $R(W)=\sum_k\sum _l\vert W \vert$

L1 정칙화는 중요하지 않은 특징을 0으로 만들어주고, L2 정칙화는 중요하지 않은 특징을 0에 가깝게 만들어주나 실제로 0이 되지는 않는다.

다음과 같이 2개의 가중치 행렬이 있다고 가정하자.

$W1=[1,0,0,0]$
$W2=[0.25,0.25,0.25,0.25]$

$[1,1,1,1]$ 의 값을 가진 데이터 X 와 $W1, W2$ 을 각각 곱하면 손실값이 동일하게 1로 나오지만 $W1$ 처럼 가중치가 한 특징에만 집중되어 있는 경우 L1 정칙화 를, $W2$ 처럼 가중치가 모든 특징에 골고루 분배되어 있으면 L2 정칙화 를 사용하는 것이 좋다.

Softmax Classifier (Multinomial Logistic Regression)

Softmax Classifier 의 손실 값은 각 클래스에 정규화 된 로그 확률 을 적용한 값이다. Softmax Classifier 의 손실함수는 다음과 같이 표현한다.

$L_i=-log(\frac{e^{s_{y_i}}}{\sum _je^{s_j}})$

식이 이해하기 어려우므로 아까와 같은 사진을 예시로 들어 설명하도록 하겠다.

아까와 다른점은 클래스별 점수가 정규화 되지 않은 로그 확률 을 나타낸다는 것이다. 먼저 고양이 사진부터 살펴보자. 고양이의 손실함수 $L_1$ 은 다음과 같은 순서로 구한다.

• 클래스별 점수에 자연함수$e$ 를 취한다.
• 자연함수를 취한 값을 정규화 시킨다.
• 정규화 시킨 값에 로그를 취한다.
• 로그를 취한 값 앞에 마이너스 부호를 붙이면 이것이 정규화 된 로그 확률 이다.

아래 사진이 위 과정을 한번에 보여준다.

위 과정을 차 사진, 개구리 사진에 마찬가지로 적용하고 각 손실 값의 평균에 정칙화 함수를 더한 값이 곧 이 분류기의 손실 값이 된다.

$L=\frac{1}{N}\sum_{i=1} L_i+R(w)$

Softmax Classifier 의 몇가지 특징을 살펴보면 다음과 같다.

Features of Softmax Classifier

1. 손실 값의 최소 값은 0, 최대 값은 무한대가 된다. 단, 손실 값이 실제로 0이 되지는 않는다.
2. 모든 클래스별 점수는 초기에는 0에 가까우므로 초기 손실 값은 $log(C)$ 의 형태를 나타낸다.

Difference and Similarity between Multiclass SVM and Softmax Classifier

• Multiclass SVM은 분류기가 이미지를 알맞게 분류하는 것에 성공했으면 더 좋은 가중치의 값을 찾는 계산을 중단한다.

• 반면 Softmax Classifier은 분류기가 이미지를 알맞게 분류하는 것에 성공했어도 더 좋은 가중치의 값을 찾기 위해 계산을 반복해 나간다.

• 그러나 두 분류기 모두 성능은 비슷하다.

Optimization

등산을 하고 있는 사람이 있다고 하자. 그 사람은 산에서 가장 고도가 낮은 지점을 찾아 내려가는 시도를 하고 있다. 산을 그래프, 사람을 손실값 으로 치환하면 이것이 바로 최적화 (optimization) 과정이다. 즉, 가장 작은 손실값을 찾는 과정이 최적화 과정이다.

최적화 과정에는 다음과 같은 알고리즘이 있다.

1. Random search: 말 그대로 랜덤하게 포인트를 찍어 그것이 최소값이길 바라는 알고리즘이다. 나쁘고 무식한 알고리즘이여서 잘 쓰이지 않는다.

2. Gradient descent: 손실함수의 한 점에서의 미분값을 구하며 기울기를 찾는 알고리즘이다. 기울기를 알면 함수가 증가/감소 하는지 알 수 있으므로 계속 반복하며 기울기를 따라가다 보면 결국 최소 손실값을 찾을 수 있게 된다. Gradient descent 에는 두 가지 방법이 있다.

   • Numerical gradient: 미분함수 공식 $\lim_{h\rightarrow0 }\frac{f(w+h)-f(w)}{h}$ 에 직접 숫자를 대입해가며 구하는 방법이다. 계산 과정이 느리고 정확하지 않지만 최적화 과정을 쉽게 이해할 수 있다는 장점이 있다.
   • Analytic gradient: 도함수, 즉 $f’(x)$를 이용하여 구하는 방법이다. 계산 과정이 빠르고 정확하지만 최적화 과정을 쉽게 이해할 수 없다는 단점이 있다.

   Gradient descent 를 파이썬 코드로 다음과 같이 나타낼 수 있다.

    while True:
        weights_grad = evaluate_gradient(loss_fun, data, weights)
        weights += -step_size * weights_grad    #step size는 포인트를 어느정도 움직일지를 나타낸다.
   

3. Stochastic Gradient Descent(SGD): 사진의 모든 픽셀에 대해 가중치 값을 구하는 것은 너무나도 복잡하고 오래 걸리는 작업이다. 따라서 일부 픽셀들만 선택해서 그 픽셀들끼리의 가중치 값을 구한다. 여기서 선택한 픽셀들을 Minibatch 라고 한다. Minibatch에 Gradient descent를 적용한 것이 Stochastic Gradient Descent 이다.

이전에 내가 수강하였던 Mathmatics for Machine Learning에 Gradient descent의 원리를 이해하기 쉽게 interactive page로 나타나 있다.

Sandpit game

Image Features

인공 신경망이 개발되기 전에는 이미지의 특정한 특징만 선택해서 이미지를 분류하는데 그 특징만이 사용되는 경우가 많았다. 사용된 대표적인 특징은 Color Spectrum(RGB), Histogram of Oriented Gradient, Bag of Words 가 있다

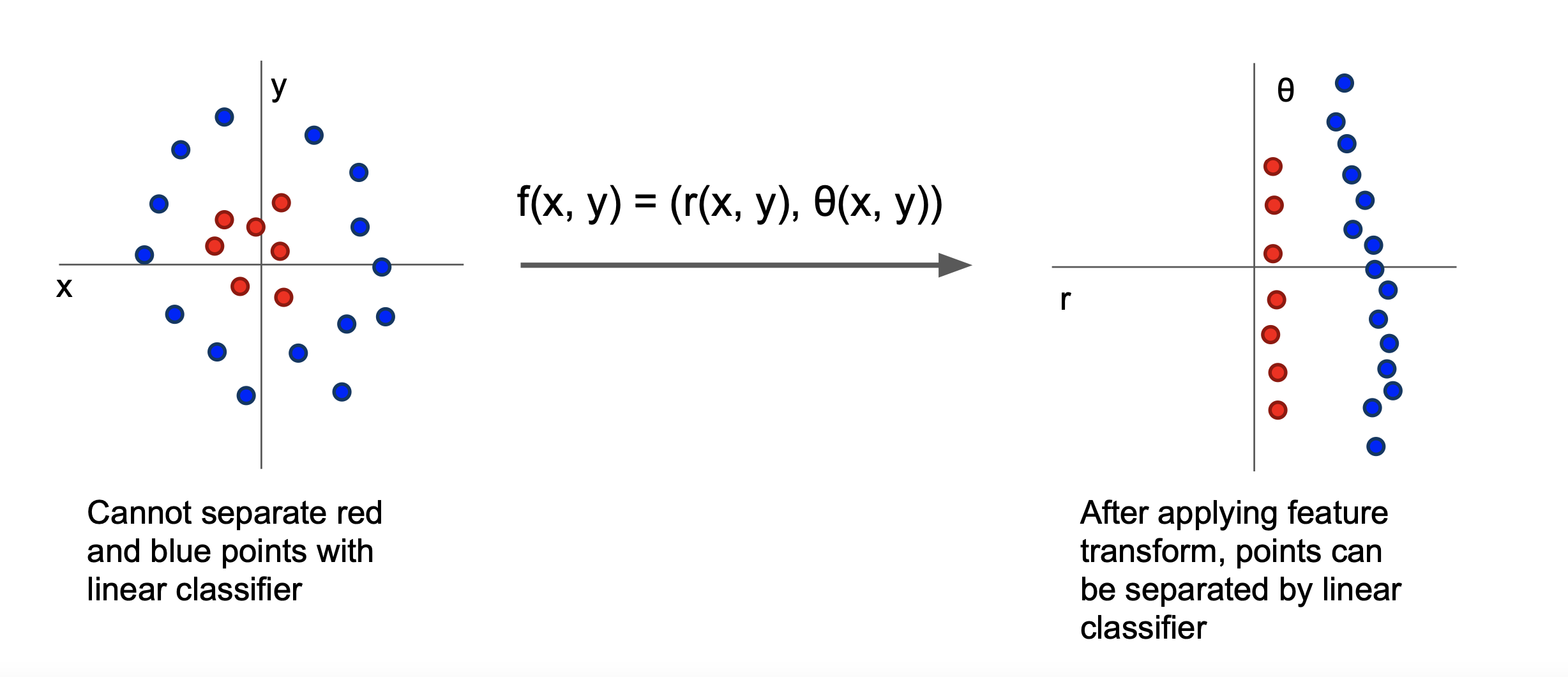
또한 왼쪽 그림에 표현된 직교 좌표계에 나타난 데이터 포인트들의 경우 빨강 포인트와 파랑 포인트를 구분하는 선형 구분선을 긋기란 쉽지 않다. 이때, 오른쪽 그림과 같이 데이터 포인트들을 극좌표로 나타내면 쉽게 선형 구분선을 그어 빨강 포인트와 파랑 포인트를 구분할 수 있다.