Chapter 4: 모델 구축 part2

본 챕터의 두 번째 파트는 신경망, 선형 모델, 랜덤 포레스트와 기타 모델등에 대해 다루고 있다.

4.4 신경망

4.4.1 신겅망의 개요

신경망의 형태는 다음과 같이 다층 퍼셉트론(MLP) 와 같은 모양을 가진다.

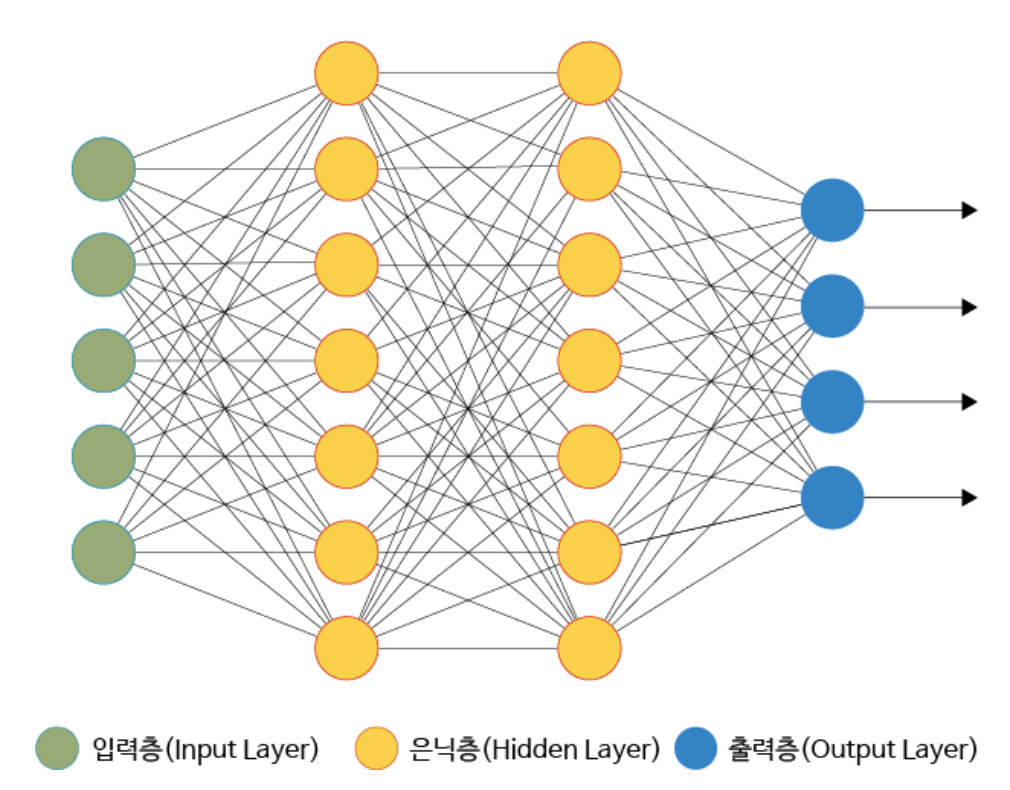
다층 퍼셉트론 모델의 특징은 다음과 같다.

• 입력층에는 특징이 입력으로 주어진다.
• 은닉 계층에서는 앞 층의 값을 가중치로 부가한 합을 구하여 결합한 뒤에 활성화 함수를 적용한다. (활성화 함수로는 relu가 자주 쓰인다).
• 출력 계층에서는 앞 층의 값을 가중치로 부가한 합을 구하여 활성화 함수를 적용한다( 회귀 문제일 때는 항등함수, 이진 분류일 때는 시그모이드 함수, 다중 클래스 분류일 때는 소프트맥스 함수 를 사용한다).

활성화 함수의 형태와 원리는 상당히 복잡하므로 신경망 모델을 전체적으로 다루는 현재 챕터에서는 집중적으로 다뤄보진 않을 것이다.

4.4.2 신경망의 특징

• 변숫값을 수치로 표헌
• 결측값을 다룰 수 없음
• 비선형성과 변수 간의 상호작용을 반영
• 변숫값을 표준화 등으로 스케일링
• 하이퍼파라미터에 따른 모델 성능의 편차가 심함
• 다중 클래스 분류에 강점
• GPU로 고속화

4.4.3 신경망의 주요 라이브러리

신경망의 주요 라이브러리에는 케라스(keras), 텐서플로(tensorflow), 파이토치(pytorch), 체이너(chainer) 등이 있다.

4.4.4 신경망의 구현

다음 코드는 신경망 모델을 구현하는 코드이다.

4.4.5 케라스 사용 팁

• 목적함수: compile 함수의 loss 매개변수에서 목적함수를 설정하고 목적함수가 최소화되도록 학습을 진행한다.
  • 회귀: mean_squared_error 으로 설정한다.
  • 이진 분류: binary_crossentropy 으로 설정한다.
  • 다중 클래스 분류: categorical_crossentropy 으로 설정한다.
• 하이퍼파라미터: 옵티마이저 종류, 합습률, 은닉 계층 수와 유닛 수, 드롭아웃 강도 등을 튜닝할 수 있다.
• 드롭아웃: 유닛 중의 일부를 몇 %로 드롭할지 지정할 수 있다.
• 학습 데이터와 검증 데이터의 점수를 출력해 학습 정도를 모니터링 할 수 있다.
• 콜백을 쓰면 학습할 때 미니배치의 처리별 또는 에폭 별로 지정한 처리를 빠르게 진행할 수 있다. 다음은 콜백을 이용해서 조기 종료를 실시하는 코드이다.

• 임베딩 게층: 양의정수를 밀집벡터로 변환하는 계층으로, 모델의 첫번째 층으로만 설정할 수 있다. 범주형 변수를 입력으로 할 때 사용할 수 있다.
• 배치 정규화: 배치 정규화 계층(BN 계층) 은 각 계층의 출력 편차를 미니배치 단위로 표준화하는 방법으로, 효과가 높아 널리 쓰인다.
• 신경망의 구조에는 다층 퍼셉트론(MLP) 이 주로 사용되었으나, 이후 순환 신경망(RNN)과 같은 구조를 이용하는 신경망이 좋은 성능을 보이므로 많이 쓰인다.

4.5 선형 모델

4.5.1 선형 모델의 개요

모델 자체만으로는 모델 성능이 그리높지 않고 특장점은 없지만 앙상블에서 하나의 모델이나 스태킹의 최종 계층에 적용하는식의 용도로 주로 쓰인다. 선형모델은 크게 분류와 회귀로 나뉜다.

• 회귀: L1 정규화를 실시하면 라소회귀, L2 정규화를 실시하면 리지회귀라고 한다.
  • L1 정규화는 특징의 계수가 완전히 0이 되는 반면, L2 정규화는 최대한 0과 가깝게 된다.
• 분류: 로지스틱 회귀 모델이 사용된다.

4.5.2 선형 모델의 특징

• 특징값은 수치로 표현
• 결측값을 다룰수 없음
• 낮은 모델 성능
• 특징 생성시 세심한 처리 필요
• 학습의 원활함을 위한 특징의 표준화 필요

4.5.3 선형 모델의 주요 라이브러리

사이킷런의 linear_model 모듈이 주로 사용되는데, 회귀 문제에서는 Ridge 클래스나 Lasso 클래스가 사용된다. 분류 문제에서는 LogisticRegression 클래스가 사용된다.

4.5.4 선형 모델의 구현

다음은 분류 문제에서의 LogisticRegression 클래스를 이용해 선형 모델을 만드는 코드이다.

4.5.5 선형 모델의 사용 팁

• 목적함수: 모델에 따라 최소화할 목적함수가 정해져 있다.
  • 회귀: 평균제곱오차(mean_squared_error)를 최소화하도록 학습한다.
  • 분류: 이진 분류일 때는 로스 손실(log_loss) 을, 다중 분류일 때는 이진 분류를 반복하는 OvR(one_vs_rest) 방법으로 학습한다.
• 하이퍼파라미터: 매개변수 C는 정규화의 강도를 나타낸다.

4.6 기타모델

4.6.1 k-최근접 이웃 알고리즘(KNN)

KNN은 행 데이터 간 거리를 그들 특징값의 차이로 정의하고, 그 거리가 가장 가까운 행 데이터 k개의 목적변수로부터 회귀 및 분류 실시한다. 사이킷런 neighbors 모듈의 KNeighborClassifier 클래스와 KNeighborRegressor 클래스가 사용된다.

4.6.2 랜덤 포레스트(RF)

다수의 결정 트리의 조합으로 예측하는 모델로, GBDT와 달리 병렬로 결정 트리를 작성한다. 각 결정 트리의 학습에서 행 데이터나 특징을 샘플링해 전달함으로써 다양한 결정 트리를 작성하고, 이들을 앙상블하여 일반화 성능이 높은 예측을 실시한다. 랜덤 포레스트의 특징은 다음과 같다.

• 사이킷런 ensemble 모듈의 분류일 때는 RandomForestClassifier 클래스, 회귀일 때는 RandomForestRegressor 클래스를 사용 한다.
• 회귀 문제일 때는 제곱오차, 분류 문제일 때는 지니 불순도가 가장 감소하도록 분기를 시행한다.
• 결정 트리마다 원래 개수와 같은 수만큼 행 데이터를 복원 추출하는 부트스트랩 샘플링을 실시한다.
• 결정 트리를 병렬로 작성하므로, GBDT와 달리 결정 트리의 개수가 지나치게 증가해 모델 성능이 낮아지는 일은 없으나 어느 정도 증가한 후에는 성능이 더 이상 올라가지 않는다.
• 부트스트랩 샘플링에서 추출되지 않은 행을 OOB(out-of-bag)라고 하는데, OOB 데이터가 검증 데이터를 대신하는 역할을 한다.

4.6.3 익스트림 랜덤 트리(ERT)

랜덤 포레스트와 거의 같은 방법으로 모델을 구축한다. 그러나 분기 작성 시 각 특징으로 데이터를 가장 잘 분할할 수 있는 임곗값을 이용하는 대신에 랜덤 설정한 임곗값을 이용한다. 랜덤 포레스트보다는 과적합하기 조금 어려운 특징을 보이고, 사이킷런 ensemble 모듈의 ExtraTreesClassifier 클래스와 ExtraTreesRegressor 클래스 를 사용한다.

4.6.4 RGF 와 FFM

• RGF(regularized greedy forest): GBDT 처럼 목적함수에 정규화항을 명시적으로 포함하지만, 작성한 결정 트리 전체에 대해 잎의 가중치를 수정하는 방법으로 결정 트리를 작성하고 성장 시킨다.

• FFM(field-aware factorization machines): 추천 문제와 잘 어울린다. libffm 와 xlearn 라이브러리가 주로 사용된다.

4.7 모델의 기타 팁과 테크닉

4.7.1 결측값이 있는 경우

결측값이 있어도 GBDT에서는 문제없이 다룰 수 있으나 결측값을 다룰 수 없는 모델은 어떻게든 결측값을 채워야 함

4.7.2 특징의 수가 많은 경우

필요 없는 특징이 학습에 포함되면 모델의 성능이 올라가지 않는다. GBDT에서는 학습만 잘 진행되면 그 나름의 결과가 나올 수 있으므로 조금씩 특징의 수를 늘려가며 어느 정도까지 학습이 가능한가 먼저 확인해보면 좋다. 만약 모델 성능에 기여하지 않는다고 판단되는 특징이 있을 땐 과감하게 삭제할 필요도 있다.

4.7.3 유사 레이블링

테스트 데이터를 학습 데이터에 더하고 다시 학습하는 것을 유사 레이블링 이라고 한다. 주로 이미지 계열 경진 대회에서 비교적 자주 활용되지만 정형 데이터에서 효과를 볼 때도 있다. 테스트 데이터 수가 학습 데이터 수보다 많으 경우 목적변수가 없더라도 테스트 데이터의 정보를 사용하고 싶을 때 유효하다. 유사 레이블링의 실행 순서는 다음과 같다.

• 학습 데이터로 학습하고 모델 구축
• ①에서 구축한 모델로 테스트 데이터 예측
• 학습 데이터에 ②의 예측값을 목적변수로 삼은 테스트 데이터를 더함
• 테스트 데이터가 추가된 학습 데이터로 다시 학습하고 모델 생성
• ④에서 구축한 모델로 테스트 데이터 예측 후 최종 예측값으로 삼음